Deck 15: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 15: Analysis of Variance
1
In testing the null hypotheses , the computed value is found by calculating
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
2
In a complete-block design
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
3
The degrees of freedom for error in a two-way ANOVA equals
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
4
The degrees of freedom for blocks in a complete-block design equals
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
In a one-factor ANOVA having three treatment levels with five observations in each sample, the between samples degrees of freedom is equal to
A) 2 .
B) 4 .
C) 12 .
D) 10 .
A) 2 .
B) 4 .
C) 12 .
D) 10 .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
A blocking factor is
A) the treatment factor in a one-way ANOVA.
B) a treatment factor ANOVA in a two-way ANOVA.
C) a factor which causes variations that are included in SSE.
D) an extraneous variable which causes variations not included in SSE.
A) the treatment factor in a one-way ANOVA.
B) a treatment factor ANOVA in a two-way ANOVA.
C) a factor which causes variations that are included in SSE.
D) an extraneous variable which causes variations not included in SSE.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
In a one-factor ANOVA having three treatment levels with five observations in each sample, the within-samples degrees of freedom equals
A) 2 .
B) 4 .
C) 12 .
D) 10
A) 2 .
B) 4 .
C) 12 .
D) 10

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
It is not true that the ratio for a one-way ANOVA
A) can be less than one.
B) must be at least zero.
C) measures .
D) involves two kinds of degrees of freedom.
A) can be less than one.
B) must be at least zero.
C) measures .
D) involves two kinds of degrees of freedom.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
If the null hypothesis in a one-way ANOVA is true, the between-samples variation is probably __________ the within-samples variation.
A) close to
B) significantly larger than
C) significantly smaller than
D) significantly different from (more or less)
A) close to
B) significantly larger than
C) significantly smaller than
D) significantly different from (more or less)

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
An experimental design in which the number of rows must equal the number of columns is provided by the
A) Latin square experiment.
B) incomplete block design.
C) complete factorial experiment.
D) two-way analysis of variance.
A) Latin square experiment.
B) incomplete block design.
C) complete factorial experiment.
D) two-way analysis of variance.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
If each kind of treatment appears with each kind of treatment once within the same block, the design is referred to as the __________ design.
A) Latin square
B) complete factorial
C) randomized block
D) balanced incomplete block
A) Latin square
B) complete factorial
C) randomized block
D) balanced incomplete block

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
The ratio which evaluates the significance of an extraneous variable in an analysis of variance is
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
Find if the degrees of freedom for treatments is 4 and the degrees of freedom for error is 12.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
Find for 4 treatments, 3 elements per sample.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
Find if the degrees of freedom for treatments is 4 the degrees of freedom for error is 12.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
Find for 4 treatments, 3 elements per sample.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
The analysis of variance table below represents part of the calculations for testing the null hypothesis . Complete the table and test the null hypothesis at .



Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
A job performance evaluator is concerned with how workers' performance ratings are affected by their skill level and their attitude. He obtained the following data:
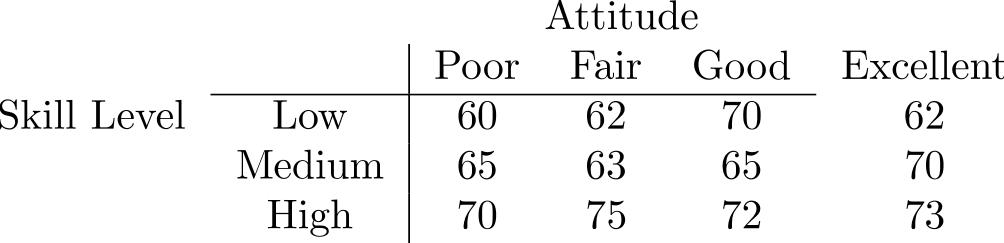 a. Construct the ANOVA table.
a. Construct the ANOVA table.
b. Test the two hypotheses at .
 a. Construct the ANOVA table.
a. Construct the ANOVA table.b. Test the two hypotheses at .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
Table 15.1
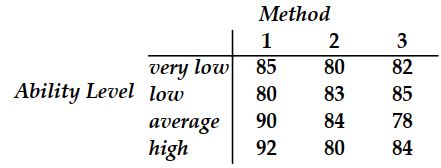
-A complete-block experiment is used to test the null hypothesis that three teaching methods produce no difference in mean achievement score. The blocking variable consists of four ability levels. Use the data in Table 15.1.
a. Construct the ANOVA table.
b. The null hypothesis of equal population means is tested at . Should it be rejected?
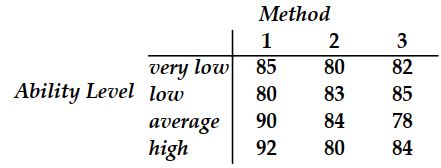
-A complete-block experiment is used to test the null hypothesis that three teaching methods produce no difference in mean achievement score. The blocking variable consists of four ability levels. Use the data in Table 15.1.
a. Construct the ANOVA table.
b. The null hypothesis of equal population means is tested at . Should it be rejected?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
A complete-block design is being used to test the null hypothesis that mean responses are identical under four treatments, with three levels used for the blocking factor.
The following data are obtained: .
a. Construct the ANOVA table.
b. Should the null hypothesis of identical population means be rejected at the significance level.
The following data are obtained: .
a. Construct the ANOVA table.
b. Should the null hypothesis of identical population means be rejected at the significance level.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
A two-factor ANOVA is being used to evaluate two null hypotheses. The first factor has 5 levels and the second has 4 levels.
The following data are obtained: .
a. Construct the ANOVA table
b. The two null hypotheses of equal means are tested at . What are the conclusions?
The following data are obtained: .
a. Construct the ANOVA table
b. The two null hypotheses of equal means are tested at . What are the conclusions?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
A new all-purpose cleaner is placed in four different locations in a supermarket. We would like to evaluate whether there is a significant difference in the number of cans sold with regard to location. The sample data below gives the number of cans sold in randomly selected supermarkets during a one-week period.
 a. Complete the one-way ANOVA table.
a. Complete the one-way ANOVA table.
b. Test whether there is a significant difference in sales of the all-purpose cleaner with regard to location. Use .
 a. Complete the one-way ANOVA table.
a. Complete the one-way ANOVA table.b. Test whether there is a significant difference in sales of the all-purpose cleaner with regard to location. Use .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
An educational researcher wants to compare four different teaching methods A, B, C, and D which she wants to try on freshmen and juniors who have three different ability levels: low (L), medium (M), and high (H). List the 24 tests she must perform so that each teaching method is used once with each combination of grade level and ability level.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
A marketing researcher wants to evaluate the success (based on resulting sales) of three different marketing strategies (I, II, III) employing three different media (radio, television, and newspapers) in three different cities: Chicago, New York, and Los Angeles.
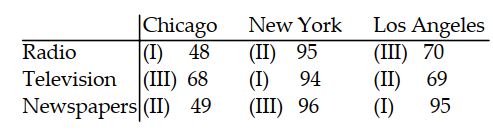 Analyze this Latin Square using the 0.05 level of significance for each test.
Analyze this Latin Square using the 0.05 level of significance for each test.
 Analyze this Latin Square using the 0.05 level of significance for each test.
Analyze this Latin Square using the 0.05 level of significance for each test.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
Under what circumstances would a Latin Square design be used in an experiment?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
What is the complete-block experiment?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
Under what circumstances would a complete-block design be a desirable design for an experiment?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
Analysis of variance is a method by which we can decide whether or not observed differences among more than two sample variances can be attributed to chance.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
If the null hypothesis in a one-way analysis of variance is false, then the variance among the sample means is larger than the variation within samples.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
The treatment sum of squares measures the variation within samples.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
The formula for SST in a two-factor experiment is the same as for a complete-block experiment.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
In a one-way analysis of variance, the null hypothesis is rejected if the obtained value is greater than the tabled value.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
The treatment sum of squares is symbolized by SST.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
A Latin Square experiment is an example of a complete factorial experiment.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
The method of analysis of variance is not applicable for data in which sample sizes are not all equal.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
In a two-way ANOVA, the degrees of freedom for treatment is calculated in the same way as that for a one-way ANOVA.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
In a Latin Square experiment, it is impossible for one factor to have three levels and another to have four levels.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
In an ratio for a one-way ANOVA, the numerator degrees of freedom is __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
In an ratio for a one-way ANOVA, the denominator degrees of freedom is __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
The __________ sum of squares measures the variation within samples.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
A two-way analysis of variance applied to an experiment in which we want to test both factors is called a __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
In a one-way ANOVA, in terms of other sums of squares, __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
A two-way ANOVA in which only one variable is of material concern, consists of one treatment factor and one __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
The __________ sum of squares measures the variation between samples.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
In a complete-block design, the sum of squares for blocks measures the variation __________ samples.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
In a complete-block design, in terms of squares, __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
In a two-factor ANOVA, in terms of squares, __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
When each kind of treatment appears together with each other kind of treatment once within the same block, the design is referred to as __________.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
In a Latin Square experiment, there are always __________ factors.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck



