Deck 5: Proofs With CP or IP
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/12
Play
Full screen (f)
Deck 5: Proofs With CP or IP
1
General Theory
-Suppose you know that a particular two-premise argument is invalid. Now suppose we add the negation of the conclusion of the two premises to form a three-sentence set of premises. Can a contradiction be derived from this three-sentence set of premises? (Defend your answer.)
-Suppose you know that a particular two-premise argument is invalid. Now suppose we add the negation of the conclusion of the two premises to form a three-sentence set of premises. Can a contradiction be derived from this three-sentence set of premises? (Defend your answer.)
No, because derivation of a contradiction would constitute an indirect proof of validity for the argument, but by the hypothesis of the problem, the argument in question is invalid.
2
General Theory
-a. Use to prove that the following argument is valid.
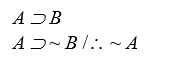 b. To illustrate how indirect proofs are a kind of shortened conditional proof, cross out the last line in the above proof and complete it as a conditional proof. (Hint: as an intermediate step prove
b. To illustrate how indirect proofs are a kind of shortened conditional proof, cross out the last line in the above proof and complete it as a conditional proof. (Hint: as an intermediate step prove 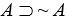 .)
.)
-a. Use to prove that the following argument is valid.
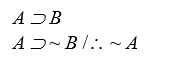 b. To illustrate how indirect proofs are a kind of shortened conditional proof, cross out the last line in the above proof and complete it as a conditional proof. (Hint: as an intermediate step prove
b. To illustrate how indirect proofs are a kind of shortened conditional proof, cross out the last line in the above proof and complete it as a conditional proof. (Hint: as an intermediate step prove 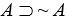 .)
.) 
3
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-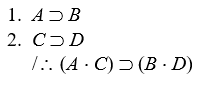
Prove valid, using the eighteen valid argument forms and CP or IP:
-
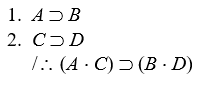
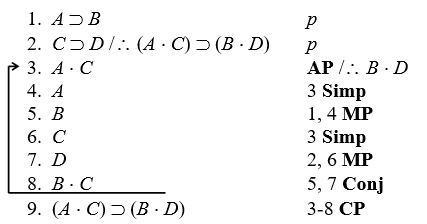
4
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-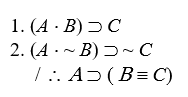
Prove valid, using the eighteen valid argument forms and CP or IP:
-
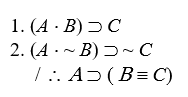

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
5
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-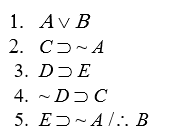
Prove valid, using the eighteen valid argument forms and CP or IP:
-
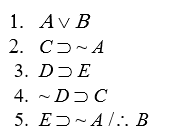

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
6
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-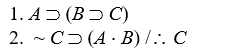
Prove valid, using the eighteen valid argument forms and CP or IP:
-

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
7
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-
Prove valid, using the eighteen valid argument forms and CP or IP:
-


Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
8
Proofs with CP or IP
Prove valid, using the eighteen valid argument forms and CP or IP:
-
Prove valid, using the eighteen valid argument forms and CP or IP:
-


Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
9
Show that premises in the following arguments are inconsistent:
-
-

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
10
Show that premises in the following arguments are inconsistent:
-
-


Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
11
Show that premises in the following arguments are inconsistent:
-
-
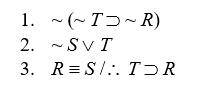

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
12
Show that premises in the following arguments are inconsistent:
-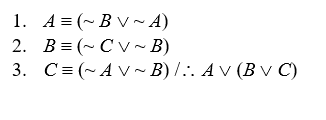
-
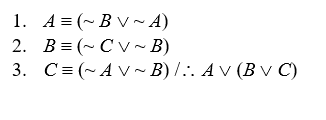

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck



