Deck 8: Predicate Logic Semantics
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/9
Play
Full screen (f)
Deck 8: Predicate Logic Semantics
1
General Theory
-If there are no unicorns, what is the truth value of the sentence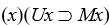 , where Ux = x is a unicorn, and Mx = x is mortal?
, where Ux = x is a unicorn, and Mx = x is mortal?
-If there are no unicorns, what is the truth value of the sentence
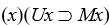 , where Ux = x is a unicorn, and Mx = x is mortal?
, where Ux = x is a unicorn, and Mx = x is mortal?The sentence 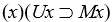 will be true. To see this, consider the expansion of this sentence for larger and larger universes of discourse. First, in a two-individual universe of discourse, its expansion is
will be true. To see this, consider the expansion of this sentence for larger and larger universes of discourse. First, in a two-individual universe of discourse, its expansion is  , which will be true since each conditional will have a false antecedent. Then for larger universes, each new conjunction added will have a false antecedent and thus be true (on the assumption nothing is a unicorn).
, which will be true since each conditional will have a false antecedent. Then for larger universes, each new conjunction added will have a false antecedent and thus be true (on the assumption nothing is a unicorn).
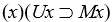 will be true. To see this, consider the expansion of this sentence for larger and larger universes of discourse. First, in a two-individual universe of discourse, its expansion is
will be true. To see this, consider the expansion of this sentence for larger and larger universes of discourse. First, in a two-individual universe of discourse, its expansion is  , which will be true since each conditional will have a false antecedent. Then for larger universes, each new conjunction added will have a false antecedent and thus be true (on the assumption nothing is a unicorn).
, which will be true since each conditional will have a false antecedent. Then for larger universes, each new conjunction added will have a false antecedent and thus be true (on the assumption nothing is a unicorn). 2
General Theory
-What about the truth value of the sentence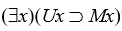 ?
?
-What about the truth value of the sentence
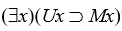 ?
?The sentence  will be true also. Again, consider its expansion for a two-individual universe, namely
will be true also. Again, consider its expansion for a two-individual universe, namely 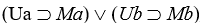 , which will be true because each conditional will have a false antecedent. And obviously, it will be true in larger universes, since adding more disjunctions to a true sentence can't make it false.
, which will be true because each conditional will have a false antecedent. And obviously, it will be true in larger universes, since adding more disjunctions to a true sentence can't make it false.
 will be true also. Again, consider its expansion for a two-individual universe, namely
will be true also. Again, consider its expansion for a two-individual universe, namely 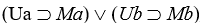 , which will be true because each conditional will have a false antecedent. And obviously, it will be true in larger universes, since adding more disjunctions to a true sentence can't make it false.
, which will be true because each conditional will have a false antecedent. And obviously, it will be true in larger universes, since adding more disjunctions to a true sentence can't make it false. 3
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-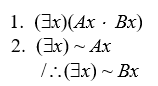
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
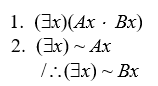
Let domain be unrestricted, Ax = x is tall, and Bx = x is identical with itself.
4
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-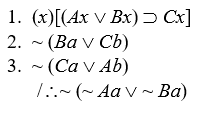
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
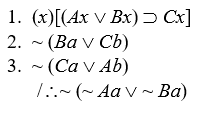

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
5
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-


Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
6
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-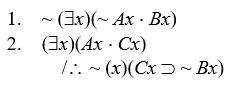
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
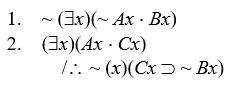

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
7
Proving invalidity
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-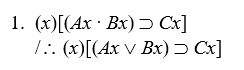
Prove that the following arguments are invalid by either the interpretation method or by the expansion method:
-
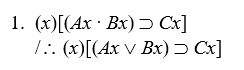

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
8
Proving consistency
Show that the premises of the arguments below are consistent.
-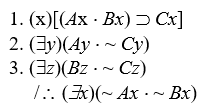
Show that the premises of the arguments below are consistent.
-
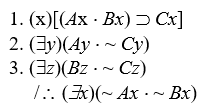

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
9
Proving consistency
Show that the premises of the arguments below are consistent.
-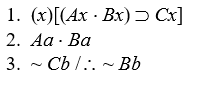
Show that the premises of the arguments below are consistent.
-
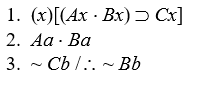

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck



