Deck 13: Identity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/22
Play
Full screen (f)
Deck 13: Identity
1
General Theory
-Determine the status of the following relations with respect to symmetry, transitivity, and reflexivity:
a) ______________ respects _ _ _ _ _ _ _ _ _
b) ______________ resembles _ _ _ _ _ _ _ _ _
c) ______________ is a child of _ _ _ _ _ _ _ _ _
-Determine the status of the following relations with respect to symmetry, transitivity, and reflexivity:
a) ______________ respects _ _ _ _ _ _ _ _ _
b) ______________ resembles _ _ _ _ _ _ _ _ _
c) ______________ is a child of _ _ _ _ _ _ _ _ _
a. nonsymmetrical, nontransitive, nonreflexive.
b. symmetrical, nontransitive, totally reflexive.
c. asymmetrical, intransitive, irreflexive.
b. symmetrical, nontransitive, totally reflexive.
c. asymmetrical, intransitive, irreflexive.
2
General Theory
-Explain why translating "s is visible to Jane" as a material conditional, such as "if s is near Jane (and the line of sight is unobstructed, etc.) then it will be seen by her," seems to be inadequate.
-Explain why translating "s is visible to Jane" as a material conditional, such as "if s is near Jane (and the line of sight is unobstructed, etc.) then it will be seen by her," seems to be inadequate.
The main problem stems from the fact that a false antecedent is sufficient for the material conditional being true. In this case then something would be visible to Jane just by the fact that it was never near her. But this could be true of something that is clearly not visible to her.
3
General Theory
-Use an example to explain the distinction that is made between sentences and propositions.
-Use an example to explain the distinction that is made between sentences and propositions.
Sentences are series of ink marks on paper or sounds in that air, and thus can be seen or heard. Examples of sentences are "Mary sees John" and "John is seen by Mary." These are each tokens of different sentence types. These sentences however express the same proposition. So it seems that propositions cannot be indentified with particular sentences, and thus seem to be a different kind of thing
4
General Theory
-Give two reasons why some think that universal statements cannot be adequately expressed as conjunctions.
-Give two reasons why some think that universal statements cannot be adequately expressed as conjunctions.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
5
Proofs with identity.
Prove the validity of the following arguments:
-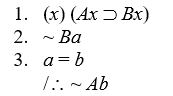
Prove the validity of the following arguments:
-
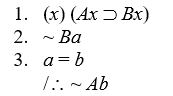

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
6
Proofs with identity.
Prove the validity of the following arguments:
-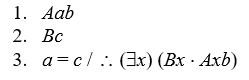
Prove the validity of the following arguments:
-
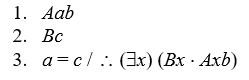

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
7
Proofs with identity.
Prove the validity of the following arguments:
-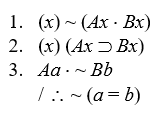
Prove the validity of the following arguments:
-
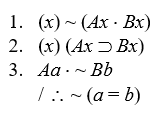

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
8
Symbolize, using the indicated letters:
-Something that is heavier than everything else is still not heavier than itself. (Hxy = "x is heavier than y ".)
-Something that is heavier than everything else is still not heavier than itself. (Hxy = "x is heavier than y ".)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
9
Symbolize, using the indicated letters:
-Anything that is heavier than itself is heavier than something else.
-Anything that is heavier than itself is heavier than something else.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
10
Symbolize, using the indicated letters:
-Any sinner who sins against someone else sins against everyone else. (Sx = "x is a sinner"; Sxy = "x sins against y".)
-Any sinner who sins against someone else sins against everyone else. (Sx = "x is a sinner"; Sxy = "x sins against y".)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
11
Symbolize, using the indicated letters:
-The sinner who sins against every sinner sins against himself.
-The sinner who sins against every sinner sins against himself.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
12
Symbolize, using the indicated letters:
-All sinners who sin against everyone else, sin against themselves.
-All sinners who sin against everyone else, sin against themselves.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
13
Symbolize, using the indicated letters:
-One and only one sinner sins against all sinners.
-One and only one sinner sins against all sinners.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
14
Symbolize, using the indicated letters:
-Not all sinners are sinned against by other sinners.
-Not all sinners are sinned against by other sinners.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
15
Symbolize, using the indicated letters:
-No sinner is sinned against by all other sinners.
-No sinner is sinned against by all other sinners.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
16
Symbolize, using the indicated letters:
-At most one sinner sins against everyone else who is a sinner. (Quite difficult)
-At most one sinner sins against everyone else who is a sinner. (Quite difficult)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
17
Symbolize, using the indicated letters:
-If some sinners are not sinned against by others, then for any nonsinners, they aren't sinned against by any sinners.
-If some sinners are not sinned against by others, then for any nonsinners, they aren't sinned against by any sinners.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
18
Symbolize, using the indicated letters:
-The largest Great Lake is Lake Superior (Gx = "x is a Great Lake"; Lxy = "x is larger than y"; s = "Lake Superior")
-The largest Great Lake is Lake Superior (Gx = "x is a Great Lake"; Lxy = "x is larger than y"; s = "Lake Superior")

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
19
Symbolize, using the indicated letters:
-The capitol of Ohio is a river town. (Cxy = "x is a capitol of y"; Rx = "x is a river town"; o = "Ohio")
-The capitol of Ohio is a river town. (Cxy = "x is a capitol of y"; Rx = "x is a river town"; o = "Ohio")

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
20
Symbolize, using the indicated letters:
-The capitol of Ohio is Columbus. (c = "Columbus")
-The capitol of Ohio is Columbus. (c = "Columbus")

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
21
Symbolize, using the indicated letters:
-The capitol of Ohio is not the largest city in Ohio. (Ixy = "x is a city in y")
-The capitol of Ohio is not the largest city in Ohio. (Ixy = "x is a city in y")

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
22
Symbolize, using the indicated letters:
-Every state has exactly two senators. (Sx = "x is a state"; Sxy = "x is a senator from y")
-Every state has exactly two senators. (Sx = "x is a state"; Sxy = "x is a senator from y")

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck



