Deck 15: Chi-Square Tests

Question 1

In a chi-square test of a 5 × 5 contingency table at α = .05, the critical value is 37.65.

Answer 1

False

Question 2

In a chi-square test for independence, observed frequencies must be at least 5 in every cell.

Answer 2

False

Question 3

The chi-square test is based on the analysis of frequencies.

Answer 3

True

Question 4

In a hypothesis test using chi-square, if the null hypothesis is true, the sample value of the sample chi-square test statistic will be exactly zero.

Question 5

The chi-square test can only be used to assess independence between two variables.

Question 6

In samples drawn from a population in which the row and column categories are independent, the value of the chi-square test statistic will be zero.

Question 7

In a chi-square test for independence, expected frequencies must be integers (or rounded to the nearest integer).

Question 8

A chi-square distribution is always skewed right.

Question 9

A large negative chi-square test statistic would indicate that the null hypothesis should be rejected.

Question 10

The chi-square test is unreliable when there are any cells with small observed frequency counts.

Question 11

The chi-square test for independence is a nonparametric test (no parameters are estimated).

Question 12

If two variables are independent, we would anticipate a chi-square test statistic close to zero.

Question 13

In a chi-square test for independence, observed and expected frequencies must sum across to the same row totals and down to the same column totals.

Question 14

Observed frequencies in a chi-square goodness-of-fit test for normality may be less than 5, or even 0, in some cells, as long as the expected frequencies are large enough.

Question 15

A chi-square test for independence is called a distribution-free test since the test is based on categorical data rather than on populations that follow any particular distribution.

Question 16

The shape of the chi-square distribution depends only on its degrees of freedom.

Question 17

Cochran's Rule requires observed frequencies of 5 or more in each cell of a contingency table.

Question 18

The degrees of freedom in a 3 × 4 chi-square contingency table would equal 11.

Question 19

The null hypothesis for a chi-square contingency test of independence for two variables always assumes that the variables are independent.

Question 20

The null hypothesis for a chi-square test on a contingency table is that the variables are dependent.

Question 21

For a chi-square goodness-of-fit test for a uniform distribution with 7 categories, we would use the critical value for 6 degrees of freedom.

Question 22

An attraction of the Kolmogorov-Smirnov test is that it is fairly easy to do without a computer.

Question 23

In a goodness-of-fit test, a linear probability plot suggests that the null hypothesis should be rejected.

Question 24

In an ECDF test for goodness-of-fit, the n observations are grouped into categories rather than being treated individually.

Question 25

The Anderson-Darling test is used to test the assumption of normality.

Question 26

In a chi-square goodness-of-fit test, a small p-value would indicate a good fit to the hypothesized distribution.

Question 27

ECDF tests have an advantage over the chi-square goodness-of-fit test on frequencies because an ECDF test treats observations individually.

Question 28

Probability plots are used to test the assumption of normality.

Question 29

For a chi-square goodness-of-fit test for a normal distribution using 7 categories with estimated mean and standard deviation, we would use the critical value for 4 degrees of freedom.

Question 30

A probability plot usually allows outliers to be detected.

Question 31

For a chi-square goodness-of-fit test for a normal distribution using 8 categories with estimated mean and standard deviation, we would use the critical value for 7 degrees of freedom.

Question 32

The Poisson goodness-of-fit test is inappropriate for continuous data.

Question 33

In a chi-square goodness-of-fit test, we lose one degree of freedom for each parameter estimated.

Question 34

The Kolmogorov-Smirnov and Anderson-Darling tests are based on the ECDF (Empirical Cumulative Distribution Function).

Question 35

When raw data are available, ECDF tests usually surpass the chi-square test in their ability to detect departures from the distribution specified in the null hypothesis.

Question 36

In a chi-square goodness-of-fit test, a sample of n observations has n - 1 degrees of freedom.

Question 37

An attraction of the Anderson-Darling test is that it is fairly easy to do without a computer.

Question 38

Goodness-of-fit tests using the ECDF (Empirical Cumulative Distribution Function) compare the actual cumulative frequencies with expected cumulative frequencies for each observation under the assumption that the data came from the hypothesized distribution.

Question 39

For a chi-square goodness-of-fit test for a uniform distribution with 5 categories, we would use the critical value for 4 degrees of freedom.

Question 40

In a chi-square goodness-of-fit test, we gain one degree of freedom if n increases by 1.

Question 41

If samples are drawn from a population that is normal, a goodness-of-fit test for normality could yield:

A)Type I error but not Type II error.
B)Type II error but not Type I error.
C)Either Type I error or Type II error.
D)Both Type I and Type II errors.

Question 42

A chi-square test of independence is a one-tailed test. The reason is that:

A)we are testing whether the frequencies exceed their expected values.
B)we square the deviations, so the test statistic lies at or above zero.
C)hypothesis tests are one-tailed tests when dealing with sample data.
D)the chi-square distribution is positively skewed.

Question 43

In a chi-square test of independence, the number of degrees of freedom equals the:

A)number of observations minus one.
B)number of categories minus one.
C)number of rows minus one times the number of columns minus one.
D)number of sample observations minus the missing observations.

Question 44

To determine how well an observed set of frequencies fits an expected set of frequencies from a Poisson distribution, we must estimate:

A)no parameters.
B)one parameter (λ).
C)two parameters (μ, σ).
D)three parameters (μ, σ, n).

Question 45

Which of these statements concerning a chi-square goodness-of-fit test is correct?

A)Data could be ratio or interval measurements.
B)Population must be normally distributed.
C)All the expected frequencies must be equal.

Question 46

We sometimes combine two row or column categories in a chi-square test when:

A)observed frequencies are more than 5.
B)observed frequencies are less than 5.
C)expected frequencies are more than 5.
D)expected frequencies are less than 5.

Question 47

In a test for a uniform distribution with k categories, the expected frequency is n/k in each cell.

Question 48

The number of cars waiting at a certain residential neighborhood stoplight is observed at 6:00 a.m. on 160 different days. The observed sample frequencies are shown here: $$\begin{array} { | l | r | r | r | r | } \hline \text { Number of cars waiting } & 0 & 1 & 2 & 3 \\\hline 60 & 60 & 50 & 30 & 20 \\\hline\end{array}$$ Under the null hypothesis of a uniform distribution, the expected number of days we would see 0 cars is:

A)10.
B)20.
C)30.
D)40.

Question 49

Kortholts that fail to meet certain precise specifications must be reworked on the next day until they are within the desired specifications. A sample of one day's output of kortholts from the Melodic Kortholt Company showed the following frequencies: $\begin{array}{|c|c|c|c|}\hline&\text { Plant A }&\text { Plant B }&\text { Row Total }\\\hline \text {Specification Met}&185 & 85&270 \\\hline \text { Specification Not Met }&15 & 15& 30\\\hline \text { Col Total }&200 & 100 &300\\\hline\end{array}$ Find the chi-square test statistic for a hypothesis of independence.

A)7.22
B)4.17
C)5.13
D)6.08

Question 50

Which of the following is not a potential solution to the problem that arises when not all expected frequencies are 5 or more in a chi-square test for independence?

A)Combine some of the columns
B)Combine some of the rows
C)Increase the sample size
D)Add more rows or columns

Question 51

The critical value in a chi-square test for independence depends on:

A)the normality of the data.
B)the variance of the data.
C)the number of categories.
D)the expected frequencies.

Question 52

Kortholts that fail to meet certain precise specifications must be reworked on the next day until they are within the desired specifications. A sample of one day's output of kortholts from the Melodic Kortholt Company showed the following frequencies: $\begin{array}{|c|c|c|c|}\hline&\text { Plant A }&\text { Plant B }&\text { Row Total }\\\hline \text {Specification Met}&185 & 85&270 \\\hline \text { Specification Not Met }&15 & 15& 30\\\hline \text { Col Total }&200 & 100 &300\\\hline\end{array}$ Find the p-value for the chi-square test statistic for a hypothesis of independence.

A)Less than .01
B)Between .01 and .025
C)Between .025 and .05
D)Greater than .05

Question 53

A chi-square goodness of fit test for a normal distribution used 40 observations, and the mean and standard deviation were estimated from the sample. The test used six categories. We would use how many degrees of freedom in looking up the critical value for the test?

A)39
B)37
C)5
D)3

Question 54

A chi-square goodness of fit test for a normal distribution used 60 observations, and the mean and standard deviation were estimated from the sample. The test used seven categories. We would use how many degrees of freedom in looking up the critical value for the test?

A)6
B)4
C)59
D)57

Question 55

A proofreader checked 160 ads for grammatical errors. The sample frequency distribution is shown: $$\begin{array} { | l | c | c | c | c | } \hline \text { Number of Errors } & 0 & 1 & 2 & 3 \\\hline \text { Observed Frequency } & 10 & 65 & 71 & 14 \\\hline\end{array}$$ Using a goodness-of-fit test to determine whether this distribution is uniform would result in a chi-square test statistic of approximately:

A)55.
B)79.
C)85.
D) 161.

Question 56

A proofreader checked 160 ads for grammatical errors. The distribution obtained is shown: $$\begin{array} { | l | c | c | c | c | } \hline \text { Number of Errors } & 0 & 1 & 2 & 3 \\\hline \text { Observed Frequency } & 10 & 65 & 71 & 14 \\\hline\end{array}$$ At ? = .01, what decision would we reach in a goodness-of-fit test to see whether this sample came from a uniform distribution?

A)Reject the null and conclude the distribution is not uniform.
B)Conclude that there is insufficient evidence to reject the null.
C)No conclusion can be made due to small expected frequencies.
D)No conclusion can be made due to inadequate sample size.

Question 57

In order to apply the chi-square test of independence, we prefer to have:

A)at least 5 observed frequencies in each cell.
B)at least 5 expected observations in each cell.
C)at least 5 percent of the observations in each cell.
D)not more than 5 observations in each cell.

Question 58

Which of these statements concerning a chi-square goodness-of-fit test is correct?

A)It is inapplicable to test for a normal distribution with open-ended top and bottom classes.
B)It is generally a better test than the chi-square test of independence.
C)There is no way to get the degrees of freedom since the right tail goes to infinity.
D)It can be used to test whether a sample follows a specified distribution.

Question 59

An operations analyst counted the number of arrivals per minute at a bank ATM in each of 30 randomly chosen minutes. The results were: 0, 3, 3, 2, 1, 0, 1, 0, 0, 1, 1, 1, 2, 1, 0, 1, 0, 1, 2, 1, 1, 2, 1, 0, 1, 2, 0, 1, 0, 1. Which goodness-of-fit test would you recommend?

A)Uniform
B)Poisson
C)Normal
D)Binomial

Question 60

A proofreader checked 160 ads for grammatical errors. The sample frequency distribution is shown: $$\begin{array} { | l | c | c | c | c | } \hline \text { Number of Errors } & 0 & 1 & 2 & 3 \\\hline \text { Observed Frequency } & 10 & 65 & 71 & 14 \\\hline\end{array}$$ Under the null hypothesis of a uniform distribution, the expected number of times we would get 0 errors is:

A)10.
B)20.
C)30.
D)40.

Question 61

To carry out a chi-square goodness-of-fit test for normality, you need at least:

A)5 categories altogether.
B)5 observations in each category.
C)5 expected observations in each category.
D)50 samples or more.

Question 62

As an independent project, a team of statistics students tabulated the types of vehicles that were parked in four different suburban shopping malls.                          $\text { MrN Location }$
$\begin{array}{|c|c|c|c|c|c|}\hline\text { Vehicle Type }& \text { Somerset } & \text { Oakland } & \text { Great Lakes } & \text { Jamestown }&\text { Row Tolal }\\\hline \text { Car }&44 & 49 & 36 & 64&193 \\\hline \text {Minivan }&21 & 15 & 18 & 13 &67\\\hline \text { Full-size Van }&2 & 3 & 3 & 2 &10\\\hline \text { SUN }&19 & 27 & 26 & 12&84 \\\hline \text {Truck }&13 & 6 & 17 & 9 &46\\\hline \text { Col Total}&100 & 100 & 100 & 100 &400\\\hline\end{array}$ For a chi-square test of independence, degrees of freedom would be:

A)20.
B)12.
C)399.
D)6.

Question 63

As an independent project, a team of statistics students tabulated the types of vehicles that were parked in four different suburban shopping malls.                          $\text { MrN Location }$
$\begin{array}{|c|c|c|c|c|c|}\hline\text { Vehicle Type }& \text { Somerset } & \text { Oakland } & \text { Great Lakes } & \text { Jamestown }&\text { Row Tolal }\\\hline \text { Car }&44 & 49 & 36 & 64&193 \\\hline \text {Minivan }&21 & 15 & 18 & 13 &67\\\hline \text { Full-size Van }&2 & 3 & 3 & 2 &10\\\hline \text { SUN }&19 & 27 & 26 & 12&84 \\\hline \text {Truck }&13 & 6 & 17 & 9 &46\\\hline \text { Col Total}&100 & 100 & 100 & 100 &400\\\hline\end{array}$ For a chi-square test of independence, the critical value for ? = .10 is:

A)10.64.
B)14.68.
C)28.41.
D)18.55.

Question 64

The table below is a tabulation of opinions of employees of Axolotl Corporation, who were sampled at random from pay records and asked to complete an anonymous job satisfaction survey.                     $\text { Degree of Satisfaction }$
$\begin{array} { |c | c | c | c | c | } \hline{ \text { Pay Type } } & \text { Satisfied } & { \text { Neutral } } & \text { Dissatisfied } & \text { Row Total } \\\hline \text { Salaried } & 40 & 10 & 10 & 60 \\\hline\text { Hourly } & 80 & 50 & 50 & 180 \\\hline \text { Col Total } & 120 & 60 & 60 & 240\\\hline\end{array}$ For a chi-square test of independence, degrees of freedom would be:

A)2
B)3
C)4
D)6

Question 65

As an independent project, a team of statistics students tabulated the types of vehicles that were parked in four different suburban shopping malls.                          $\text { MrN Location }$
$\begin{array}{|c|c|c|c|c|c|}\hline\text { Vehicle Type }& \text { Somerset } & \text { Oakland } & \text { Great Lakes } & \text { Jamestown }&\text { Row Tolal }\\\hline \text { Car }&44 & 49 & 36 & 64&193 \\\hline \text {Minivan }&21 & 15 & 18 & 13 &67\\\hline \text { Full-size Van }&2 & 3 & 3 & 2 &10\\\hline \text { SUN }&19 & 27 & 26 & 12&84 \\\hline \text {Truck }&13 & 6 & 17 & 9 &46\\\hline \text { Col Total}&100 & 100 & 100 & 100 &400\\\hline\end{array}$ Assuming independence, the expected frequency of SUVs in Jamestown is:

A)12.
B)21.
C)75.
D)60.

Question 66

Employees of OxCo Mfg. were surveyed to evaluate the company's pension plan. The table below displays some of the results of the survey. 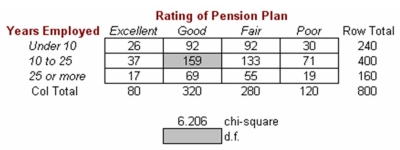The expected frequency for the shaded cell in the table would be:

A)163.
B)158.
C)165.
D) 160.

Question 67

The table below is a tabulation of opinions of employees of Axolotl Corporation, who were sampled at random from pay records and asked to complete an anonymous job satisfaction survey.                     $\text { Degree of Satisfaction }$
$\begin{array} { |c | c | c | c | c | } \hline{ \text { Pay Type } } & \text { Satisfied } & { \text { Neutral } } & \text { Dissatisfied } & \text { Row Total } \\\hline \text { Salaried } & 40 & 10 & 10 & 60 \\\hline\text { Hourly } & 80 & 50 & 50 & 180 \\\hline \text { Col Total } & 120 & 60 & 60 & 240\\\hline\end{array}$ Assuming independence, the expected frequency of satisfied hourly employees is:

A)80.
B)90.
C)75.
D)60.

Question 68

An operations analyst counted the number of arrivals per minute at an ATM in each of 30 randomly chosen minutes. The results were: 0, 3, 3, 2, 1, 0, 1, 0, 0, 1, 1, 1, 2, 1, 0, 1, 0, 1, 2, 1, 1, 2, 1, 0, 1, 2, 0, 1, 0, 1. For the Poisson goodness-of-fit test, what is the expected frequency of the data value X = 1?

A)Impossible to determine.
B)11.04
C)1.00
D)2.47

Question 69

The table below is a tabulation of opinions of employees of Axolotl Corporation, who were sampled at random from pay records and asked to complete an anonymous job satisfaction survey.                     $\text { Degree of Satisfaction }$
$\begin{array} { |c | c | c | c | c | } \hline{ \text { Pay Type } } & \text { Satisfied } & { \text { Neutral } } & \text { Dissatisfied } & \text { Row Total } \\\hline \text { Salaried } & 40 & 10 & 10 & 60 \\\hline\text { Hourly } & 80 & 50 & 50 & 180 \\\hline \text { Col Total } & 120 & 60 & 60 & 240\\\hline\end{array}$ For a chi-square test of independence, the critical value for ? = .01 is:

A)9.210.
B)4.605.
C)11.34.
D)16.81.

Question 70

You test a hypothesis of independence of two variables. The number of observations is 500 and you have classified the data into a 4 by 4 contingency table. The test statistic has __________ degrees of freedom.

A)16
B)9
C)499
D)498

Question 71

Students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Their replies are summarized below.                          $\text { Degree of Certainty }$
$\begin{array} { |c | c | c | c | c | } \hline \text { Credits Earned }&{ \text { Very Uncertain } } & \text { Somewhat Certain } & { \text { Very Certain} } & \text { Row Tot } \\\hline \text {Under 10 } & 14 & 16 & 6 &46 \\\hline\text { 10 through 59} & 16& 8 & 20 & 44 \\\hline \text { 60 or more } & 2 & 14 & 22 & 38\\\hline \text { Col Total } & 42 & 38 & 48 & 128\\\hline\end{array}$ Assuming independence, the expected frequency of very uncertain students with 60 credits or more is:

A)12.47.
B)2.00.
C)14.56.
D)11.09.

Question 72

You want to test the hypothesis that the prime rate and inflation are independent. The following table is prepared for the test on the basis of the results of a random sample, collected in various countries and various time periods: 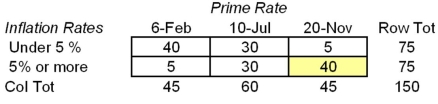Using α = .05, what is the critical value of the test statistic that you would use?

A)3.841
B)12.59
C)5.991
D)7.815

Question 73

Students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Their replies are summarized below.                          $\text { Degree of Certainty }$
$\begin{array} { |c | c | c | c | c | } \hline \text { Credits Earned }&{ \text { Very Uncertain } } & \text { Somewhat Certain } & { \text { Very Certain} } & \text { Row Tot } \\\hline \text {Under 10 } & 14 & 16 & 6 &46 \\\hline\text { 10 through 59} & 16& 8 & 20 & 44 \\\hline \text { 60 or more } & 2 & 14 & 22 & 38\\\hline \text { Col Total } & 42 & 38 & 48 & 128\\\hline\end{array}$ For a chi-square test of independence, degrees of freedom would be:

A)2.
B)9.
C)4.
D)127.

Question 74

Students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Their replies are summarized below.                          $\text { Degree of Certainty }$
$\begin{array} { |c | c | c | c | c | } \hline \text { Credits Earned }&{ \text { Very Uncertain } } & \text { Somewhat Certain } & { \text { Very Certain} } & \text { Row Tot } \\\hline \text {Under 10 } & 14 & 16 & 6 &46 \\\hline\text { 10 through 59} & 16& 8 & 20 & 44 \\\hline \text { 60 or more } & 2 & 14 & 22 & 38\\\hline \text { Col Total } & 42 & 38 & 48 & 128\\\hline\end{array}$ Under the assumption of independence, the expected frequency in the upper left cell is:

A)15.09.
B)24.00.
C)19.72.
D)20.22.

Question 75

Employees of OxCo Mfg. were surveyed to evaluate the company's pension plan. The table below displays some of the results of the survey. 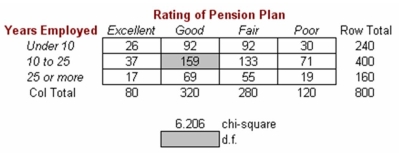The appropriate conclusion would be:

A)do not reject H₀.
B)reject H₀ at α = .10.
C)reject H₀ at α = .05.
D)reject H₀ at α = .01.

Question 76

Employees of OxCo Mfg. were surveyed to evaluate the company's pension plan. The table below displays some of the results of the survey. 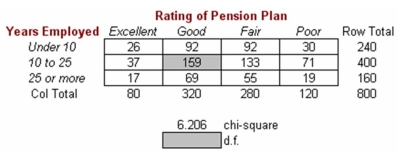Degrees of freedom for this test (shaded cell below the table) would be:

A)6.
B)7.
C)799.
D)12.

Question 77

You want to test the hypothesis that the prime rate and inflation are independent. The following table is prepared for the test on the basis of the results of a random sample, collected in various countries and various time periods: The expected frequency for the shaded cell is:

A)22.5.
B)30.
C)40.
D)40.5.

Question 78

You want to test the hypothesis that the prime rate and inflation are independent. The following table is prepared for the test on the basis of the results of a random sample, collected in various countries and various time periods: 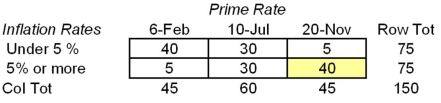What is the value of the test statistic?

A)306.25
B)0.00
C)54.44
D)13.61

Question 79

Students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Their replies are summarized below.                          $\text { Degree of Certainty }$
$\begin{array} { |c | c | c | c | c | } \hline \text { Credits Earned }&{ \text { Very Uncertain } } & \text { Somewhat Certain } & { \text { Very Certain} } & \text { Row Tot } \\\hline \text {Under 10 } & 14 & 16 & 6 &46 \\\hline\text { 10 through 59} & 16& 8 & 20 & 44 \\\hline \text { 60 or more } & 2 & 14 & 22 & 38\\\hline \text { Col Total } & 42 & 38 & 48 & 128\\\hline\end{array}$ For a chi-square test of independence, the critical value for ? = .05 is:

A)5.991.
B)7.815.
C)9.488.
D)16.92.

Question 80

Students in an introductory college economics class were asked how many credits they had earned in college, and how certain they were about their choice of major. Their replies are summarized below.                          $\text { Degree of Certainty }$
$\begin{array} { |c | c | c | c | c | } \hline \text { Credits Earned }&{ \text { Very Uncertain } } & \text { Somewhat Certain } & { \text { Very Certain} } & \text { Row Tot } \\\hline \text {Under 10 } & 14 & 16 & 6 &46 \\\hline\text { 10 through 59} & 16& 8 & 20 & 44 \\\hline \text { 60 or more } & 2 & 14 & 22 & 38\\\hline \text { Col Total } & 42 & 38 & 48 & 128\\\hline\end{array}$ Which statement is most nearly correct?

A)The contingency table violates Cochran's Rule.
B)Visual inspection of column frequencies suggests independence.
C)At ? = .05 we would easily reject the null hypothesis of independence.
D)At ? = .05 we cannot reject he null hypothesis of independence.