Deck 11: Statistical Inference Concerning Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/120
Play
Full screen (f)
Deck 11: Statistical Inference Concerning Variance
1
We can use Excel's function ________ that returns the right-tailed probability of the chi-square distribution.
CHISQ.DIST.RT
2
Statistical inference for σ2 is based on the F distribution.
False
3
The null hypothesis H0: σ2 ≤ 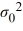 is rejected if the value of the test statistic exceeds
is rejected if the value of the test statistic exceeds 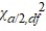 .
.
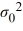 is rejected if the value of the test statistic exceeds
is rejected if the value of the test statistic exceeds 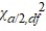 .
.True
4
Use the R function ________ to obtain left-tail probabilities of the chi-square distribution.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
5
The values of the 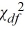 distribution range from negative infinity to infinity.
distribution range from negative infinity to infinity.
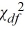 distribution range from negative infinity to infinity.
distribution range from negative infinity to infinity.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
6
The population variance is one of the most widely used quantitative measures of risk in investments.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
7
The skewness of the chi-square distribution depends on the degrees of freedom.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
8
The formula for constructing the confidence interval for the ratio of two population variances is based on the assumption that the sample variances are computed from independently drawn samples from two non-normally distributed populations.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
9
In general, the 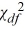 distribution is the probability distribution of the sum of several independent squared standard ________ random variables.
distribution is the probability distribution of the sum of several independent squared standard ________ random variables.
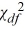 distribution is the probability distribution of the sum of several independent squared standard ________ random variables.
distribution is the probability distribution of the sum of several independent squared standard ________ random variables.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
10
Inference for two population variances is done through their difference 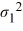 -
- 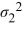 .
.
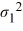 -
- 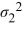 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
11
The estimator of 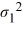 /
/ 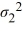 used in the inference regarding the ratio of two population variances is
used in the inference regarding the ratio of two population variances is 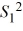 /
/ 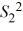 .
.
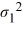 /
/ 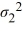 used in the inference regarding the ratio of two population variances is
used in the inference regarding the ratio of two population variances is 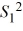 /
/ 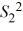 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
12
The 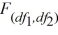 distribution is negatively skewed.
distribution is negatively skewed.
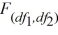 distribution is negatively skewed.
distribution is negatively skewed.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
13
A right-tailed test for the ratio of two population variances Η0: 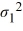 /
/ 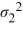 ≤ 1 examines whether
≤ 1 examines whether 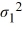 is greater than
is greater than 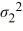 .
.
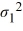 /
/ 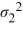 ≤ 1 examines whether
≤ 1 examines whether 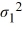 is greater than
is greater than 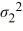 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
14
The value of the test statistic for the hypothesis test of the population variance, σ2 is computed as 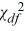 =
= 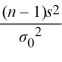 .
.
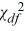 =
= 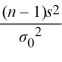 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
15
For a test about the ratio of two population variances, the test statistic is given by 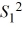 /
/ 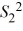 .
.
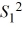 /
/ 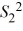 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
16
The relevant value in the ________ tail of the 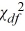 distribution is
distribution is 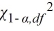 .
.
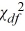 distribution is
distribution is 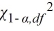 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
17
It is preferable to place the smaller sample variance in the numerator of the 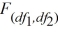 statistic.
statistic.
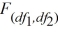 statistic.
statistic.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
18
The formula for the confidence interval of the population variance σ2 is valid for the random samples drawn from any population.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
19
The sampling distribution of 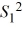 /
/ 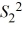 is the χ2 distribution.
is the χ2 distribution.
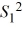 /
/ 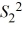 is the χ2 distribution.
is the χ2 distribution.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
20
The formula for the confidence interval of the population variance σ2 is valid only when the random sample is drawn from a ________ distributed population.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
21
The F distribution depends on ________ degrees of freedom.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
22
If s2 is computed from a random sample of n observations drawn from an underlying normal population with a finite variance, then the 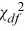 variable is defined as
variable is defined as
A)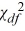 =
= 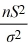 .
.
B)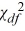 =
= 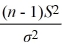 .
.
C)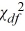 =
= 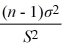 .
.
D)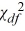 =
= 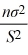 .
.
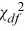 variable is defined as
variable is defined asA)
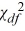 =
= 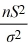 .
.B)
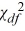 =
= 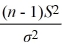 .
.C)
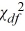 =
= 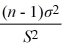 .
.D)
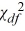 =
= 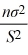 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
23
The ________ is the probability distribution of the sum of several independent squared standard normal random variables.
A) F distribution
B) distribution
distribution
C) student's t distribution
D) uniform distribution
A) F distribution
B)
 distribution
distributionC) student's t distribution
D) uniform distribution

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
24
The Excel's function ________ returns the p-value for a right-tailed test for the ratio of two population variances.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following is a 98% confidence interval for the population variance when the sample variance is 20 for a sample of 10 items from a normal population?
A) [8.308, 86.207]
B) [7.476, 77.512]
C) [8.617, 78.125]
D) [7.755, 70.313]
A) [8.308, 86.207]
B) [7.476, 77.512]
C) [8.617, 78.125]
D) [7.755, 70.313]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
26
As the df grow larger, the 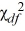 distribution approaches the
distribution approaches the
A) F distribution
B) uniform distribution
C) student's t distribution
D) normal distribution
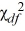 distribution approaches the
distribution approaches theA) F distribution
B) uniform distribution
C) student's t distribution
D) normal distribution

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following is a feature of the F distribution?
A) The F distribution depends on one degree of freedom.
B) The F distribution is bell-shaped with values ranging from negative infinity to infinity.
C) The F distribution becomes increasingly symmetric when the degrees of freedom increase.
D) The F distribution is negatively skewed.
A) The F distribution depends on one degree of freedom.
B) The F distribution is bell-shaped with values ranging from negative infinity to infinity.
C) The F distribution becomes increasingly symmetric when the degrees of freedom increase.
D) The F distribution is negatively skewed.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following is used to conduct a hypothesis test about the population variance?
A) Sample mean
B) Population mean
C) Sample proportion
D) Sample variance
A) Sample mean
B) Population mean
C) Sample proportion
D) Sample variance

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
29
If a sample of size n is taken from a normal population with a finite variance, then the statistic 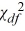 =
= 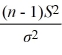 follows the
follows the 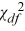 distribution with degrees of freedom.
distribution with degrees of freedom.
A) (n + 1)(n − 1).
B) n + 1.
C) n − 1.
D) n.
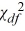 =
= 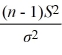 follows the
follows the 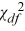 distribution with degrees of freedom.
distribution with degrees of freedom.A) (n + 1)(n − 1).
B) n + 1.
C) n − 1.
D) n.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
30
The specification of the confidence interval for the ratio of two population variances is based on the assumption that the sample variances are computed from ________ drawn samples from two normally distributed populations.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
31
If P( 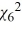 ≥ x) = 0.05, then the value of x is
≥ x) = 0.05, then the value of x is
A) 14.449.
B) 10.645.
C) 12.592.
D) 1.6350.
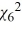 ≥ x) = 0.05, then the value of x is
≥ x) = 0.05, then the value of x isA) 14.449.
B) 10.645.
C) 12.592.
D) 1.6350.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following is the value of 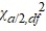 for a 99% confidence level and degrees of freedom equal 6?
for a 99% confidence level and degrees of freedom equal 6?
A) 16.812
B) 18.548
C) 0.872
D) 0.676
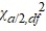 for a 99% confidence level and degrees of freedom equal 6?
for a 99% confidence level and degrees of freedom equal 6?A) 16.812
B) 18.548
C) 0.872
D) 0.676

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
33
All F(
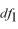 ,
, 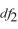 ) distributions are ________ skewed.
) distributions are ________ skewed.
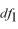 ,
, 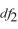 ) distributions are ________ skewed.
) distributions are ________ skewed.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
34
The values taken from a normally distributed population are 21 23 25 27 28 35 30 32 33.
Which of the following is a 95% confidence interval for the population variance?
A) [2.03, 16.30]
B) [10.12, 81.43]
C) [9.00, 72.41]
D) [11.39, 91.64]
Which of the following is a 95% confidence interval for the population variance?
A) [2.03, 16.30]
B) [10.12, 81.43]
C) [9.00, 72.41]
D) [11.39, 91.64]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
35
For a sample of 10 observations drawn from a normally distributed population, we obtain the sample mean and the sample variance as 50 and 75, respectively. We want to determine whether the population variance is greater than 70. The 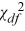 test statistic is
test statistic is
A) 1.645.
B) 3.325.
C) 9.642.
D) 16.919.
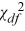 test statistic is
test statistic isA) 1.645.
B) 3.325.
C) 9.642.
D) 16.919.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following is the formula for the sample variance s2 when used as an estimate of σ2 for a random sample of n observations from a population?
A) s2 =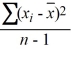
B) s2 =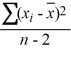
C) s2 =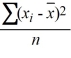
D) s2 =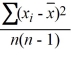
A) s2 =
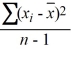
B) s2 =
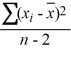
C) s2 =
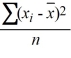
D) s2 =
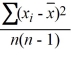

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
37
Statistical inference about σ2 is based on which of the following distributions?
A) The F distribution
B) The student's t distribution
C) The chi-square distribution
D) The normal distribution
A) The F distribution
B) The student's t distribution
C) The chi-square distribution
D) The normal distribution

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
38
Use the R function ________ to obtain a p-value for a test about the ratio of two population variances.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following hypotheses is a right-tail test about the population variance?
A) Η0: σ2 =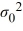 , ΗA: σ2 ≠
, ΗA: σ2 ≠ 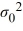
B) Η0: σ2 ≤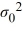 , ΗA: σ2 >
, ΗA: σ2 > 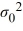
C) Η0: σ2 >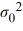 , ΗA: σ2 <
, ΗA: σ2 < 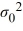
D) Η0: σ2 ≥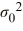 , ΗA: σ2 >
, ΗA: σ2 > 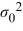
A) Η0: σ2 =
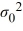 , ΗA: σ2 ≠
, ΗA: σ2 ≠ 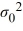
B) Η0: σ2 ≤
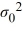 , ΗA: σ2 >
, ΗA: σ2 > 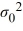
C) Η0: σ2 >
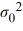 , ΗA: σ2 <
, ΗA: σ2 < 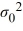
D) Η0: σ2 ≥
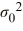 , ΗA: σ2 >
, ΗA: σ2 > 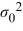

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
40
You want to test whether the population variance differs from 50. From a sample of 25 observations drawn from a normally distributed population, you calculate s2 = 80. When conducting this test at the 5% significance level, the, 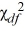 critical value is
critical value is
A) 5.625.
B) 12.401.
C) 14.400.
D) 39.364.
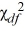 critical value is
critical value isA) 5.625.
B) 12.401.
C) 14.400.
D) 39.364.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the following Excel functions is used to calculate the exact left-tail probability for a 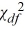 distribution?
distribution?
A) CHISQ.DIST(x, Deg_freedom, Cumulative)
B) CHISQ.DIST(x, n−2)
C) CHISQ.DIST(x, n/2)
D) CHISQ.DIST(x/2, Deg_freedom, Cumulative)
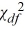 distribution?
distribution?A) CHISQ.DIST(x, Deg_freedom, Cumulative)
B) CHISQ.DIST(x, n−2)
C) CHISQ.DIST(x, n/2)
D) CHISQ.DIST(x/2, Deg_freedom, Cumulative)

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
42
A random sample of 18 observations is taken from a normal population. The sample mean and sample standard deviation are 76.4 and 4.2, respectively. What is an 80% interval estimate of the population variance?
A) [12.107, 29.735]
B) [10.870, 34.581]
C) [12.819, 31.484]
D) [14.636, 23.443]
A) [12.107, 29.735]
B) [10.870, 34.581]
C) [12.819, 31.484]
D) [14.636, 23.443]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
43
A professor wants to compare the variances of scores between two sections of classes. The students in each section took the same test. The random samples yield sample variances of ![<strong>A professor wants to compare the variances of scores between two sections of classes. The students in each section took the same test. The random samples yield sample variances of = 203.15 and = 474.42 for samples of n<sub>1</sub> = 13 and n<sub>2</sub> = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?</strong> A) [0.1540, 2.7809] B) [0.1008, 2.0217] C) [0.1386, 3.0895] D) [0.0907, 1.8198]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e8_456f_b223_cbe75b53084a_TB6618_11.jpg) = 203.15 and
= 203.15 and ![<strong>A professor wants to compare the variances of scores between two sections of classes. The students in each section took the same test. The random samples yield sample variances of = 203.15 and = 474.42 for samples of n<sub>1</sub> = 13 and n<sub>2</sub> = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?</strong> A) [0.1540, 2.7809] B) [0.1008, 2.0217] C) [0.1386, 3.0895] D) [0.0907, 1.8198]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e8_6c80_b223_c5298ef71df2_TB6618_11.jpg) = 474.42 for samples of n1 = 13 and n2 = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?
= 474.42 for samples of n1 = 13 and n2 = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?
A) [0.1540, 2.7809]
B) [0.1008, 2.0217]
C) [0.1386, 3.0895]
D) [0.0907, 1.8198]
![<strong>A professor wants to compare the variances of scores between two sections of classes. The students in each section took the same test. The random samples yield sample variances of = 203.15 and = 474.42 for samples of n<sub>1</sub> = 13 and n<sub>2</sub> = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?</strong> A) [0.1540, 2.7809] B) [0.1008, 2.0217] C) [0.1386, 3.0895] D) [0.0907, 1.8198]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e8_456f_b223_cbe75b53084a_TB6618_11.jpg) = 203.15 and
= 203.15 and ![<strong>A professor wants to compare the variances of scores between two sections of classes. The students in each section took the same test. The random samples yield sample variances of = 203.15 and = 474.42 for samples of n<sub>1</sub> = 13 and n<sub>2</sub> = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?</strong> A) [0.1540, 2.7809] B) [0.1008, 2.0217] C) [0.1386, 3.0895] D) [0.0907, 1.8198]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e8_6c80_b223_c5298ef71df2_TB6618_11.jpg) = 474.42 for samples of n1 = 13 and n2 = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?
= 474.42 for samples of n1 = 13 and n2 = 16, respectively. Which of the following is a 99% confidence interval for the ratio of the population variances?A) [0.1540, 2.7809]
B) [0.1008, 2.0217]
C) [0.1386, 3.0895]
D) [0.0907, 1.8198]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
44
How does the width of the interval respond to the changes in the confidence level?
A) The width of the interval decreases with an increase in the confidence level.
B) The width of the interval increases with an increase in the confidence level.
C) The width of the interval is halved with the increase in the confidence level.
D) The width of the interval is doubled with the decrease in the confidence level.
A) The width of the interval decreases with an increase in the confidence level.
B) The width of the interval increases with an increase in the confidence level.
C) The width of the interval is halved with the increase in the confidence level.
D) The width of the interval is doubled with the decrease in the confidence level.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
45
If independent samples of size n1 and n2 are drawn from normal populations with equal variances, then the value of the 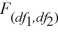 statistic is calculated as
statistic is calculated as
A)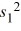 ×
× 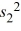 .
.
B)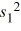 /
/ 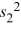 .
.
C)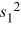 (n1 - 1) ×
(n1 - 1) × 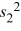 (n2 - 1).
(n2 - 1).
D)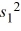
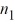 /
/ 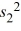
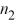 .
.
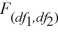 statistic is calculated as
statistic is calculated asA)
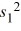 ×
× 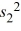 .
.B)
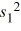 /
/ 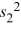 .
.C)
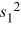 (n1 - 1) ×
(n1 - 1) × 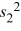 (n2 - 1).
(n2 - 1).D)
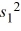
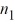 /
/ 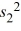
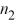 .
.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following are the degrees of freedom df1 and df2 for an 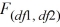 distribution?
distribution?
A) (n1 − 2); (n2 − 2)
B) n2(n1 − 2); n1(n2 − 2)
C) (n1 − 1); (n2 − 1)
D) n(n1 − 1); n(n2 − 1)
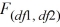 distribution?
distribution?A) (n1 − 2); (n2 − 2)
B) n2(n1 − 2); n1(n2 − 2)
C) (n1 − 1); (n2 − 1)
D) n(n1 − 1); n(n2 − 1)

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
47
The manager of a video library would like the variance of the waiting times of the customers not to exceed 2.30 minutes-squared. He would like to add an additional billing counter if the variance exceeds the cut-off. He checks the recent sample data. For a random sample of 24 customer waiting times, he arrives at a sample variance of 3.8 minutes-squared. The manager assumes the waiting times to be normally distributed. At α = 0.05, which of the following is the critical value 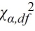 ?
?
A) 13.091
B) 32.007
C) 35.172
D) 38.076
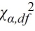 ?
?A) 13.091
B) 32.007
C) 35.172
D) 38.076

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
48
Which of the following characteristics is true regarding the F distribution?
A) The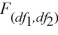 distribution is negatively skewed.
distribution is negatively skewed.
B) The values of the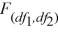 distribution range from negative infinity to infinity.
distribution range from negative infinity to infinity.
C) The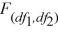 distribution is the probability distribution of the ratio of two independent chi-square variables.
distribution is the probability distribution of the ratio of two independent chi-square variables.
D) The shape of the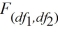 distribution is independent of the degrees of freedom.
distribution is independent of the degrees of freedom.
A) The
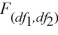 distribution is negatively skewed.
distribution is negatively skewed.B) The values of the
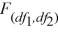 distribution range from negative infinity to infinity.
distribution range from negative infinity to infinity.C) The
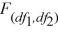 distribution is the probability distribution of the ratio of two independent chi-square variables.
distribution is the probability distribution of the ratio of two independent chi-square variables.D) The shape of the
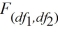 distribution is independent of the degrees of freedom.
distribution is independent of the degrees of freedom.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
49
The manager of a video library would like the variance of the waiting times of the customers not to exceed 2.30 minutes-squared. He would like to add an additional billing counter if the variance exceeds the cut-off. He checks the recent sample data. For a random sample of 24 customer waiting times, he arrives at a sample variance of 3.8 minutes-squared. The manager assumes the waiting times to be normally distributed. Which of the following would be null and the alternate hypothesis to test if the cut-off is surpassed?
A) Η0: σ2 ≤ 2.3, ΗA: σ2 > 2.3.
B) Η0: σ2 = 2.3, ΗA: σ2 ≠ 2.3.
C) Η0: σ2 ≥2.3, ΗA: σ2 < 2.3.
D) Η0: σ2 < 2.3, ΗA: σ2 ≥ 2.3.
A) Η0: σ2 ≤ 2.3, ΗA: σ2 > 2.3.
B) Η0: σ2 = 2.3, ΗA: σ2 ≠ 2.3.
C) Η0: σ2 ≥2.3, ΗA: σ2 < 2.3.
D) Η0: σ2 < 2.3, ΗA: σ2 ≥ 2.3.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
50
For a two-tailed test about two population variances, the null hypothesis is given by
A)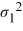 = 1 /
= 1 / 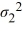 .
.
B)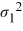 - 1 =
- 1 = 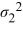 .
.
C)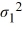 +
+ 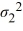 = 1.
= 1.
D)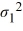 /
/ 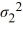 = 1.
= 1.
A)
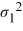 = 1 /
= 1 / 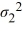 .
.B)
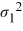 - 1 =
- 1 = 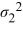 .
.C)
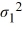 +
+ 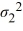 = 1.
= 1.D)
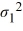 /
/ 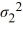 = 1.
= 1.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
51
Becky owns a diner and is concerned about sustaining the business. She wants to ascertain if the standard deviation of the profits for each week is greater than $250. The details of the profits for the week are (in dollars) 1,743 1,438 1,212 1,705 1,985 1,857 1,916
Assume that profits are normally distributed. Which of the following are appropriate hypotheses to test Becky's concern?
A) Η0: σ2 = 62,500, ΗA: σ2 ≠ 62,500
B) Η0: σ2 < 62,500, ΗA: σ2 ≥ 62,500
C) Η0: σ2 ≤ 62,500, ΗA: σ2 > 62,500
D) Η0: σ2 ≥ 62,500, ΗA: σ2 < 62,500
Assume that profits are normally distributed. Which of the following are appropriate hypotheses to test Becky's concern?
A) Η0: σ2 = 62,500, ΗA: σ2 ≠ 62,500
B) Η0: σ2 < 62,500, ΗA: σ2 ≥ 62,500
C) Η0: σ2 ≤ 62,500, ΗA: σ2 > 62,500
D) Η0: σ2 ≥ 62,500, ΗA: σ2 < 62,500

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
52
Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n1 = 11 and n2 = 16 with sample variances of 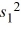 = 400 and
= 400 and 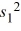 = 200, respectively. Suppose you obtain a 95% confidence for the ratio of the population variances. Which of the below allows you to conclude the first variance is smaller than the second variance?
= 200, respectively. Suppose you obtain a 95% confidence for the ratio of the population variances. Which of the below allows you to conclude the first variance is smaller than the second variance?
A) The entire interval is less than 1
B) The interval captures 1
C) The entire interval is more than 1
D) None of the above
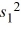 = 400 and
= 400 and 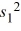 = 200, respectively. Suppose you obtain a 95% confidence for the ratio of the population variances. Which of the below allows you to conclude the first variance is smaller than the second variance?
= 200, respectively. Suppose you obtain a 95% confidence for the ratio of the population variances. Which of the below allows you to conclude the first variance is smaller than the second variance?A) The entire interval is less than 1
B) The interval captures 1
C) The entire interval is more than 1
D) None of the above

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
53
Which of the following R functions is used to calculate the exact left-tail probability for a 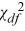 distribution?
distribution?
A) 1-pchisq(x, df)
B) 1-pchisq(x, df, lower.tail=TRUE)
C) pchisq(x, df)
D) None of the above
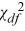 distribution?
distribution?A) 1-pchisq(x, df)
B) 1-pchisq(x, df, lower.tail=TRUE)
C) pchisq(x, df)
D) None of the above

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
54
The manager of a video library would like the variance of the waiting times of the customers not to exceed 2.30 minutes-squared. He would like to add an additional billing counter if the variance exceeds the cut-off. He checks the recent sample data. For a random sample of 24 customer waiting times, he arrives at a sample variance of 3.8 minutes-squared. The manager assumes the waiting times to be normally distributed. Which of the following is the correct approximation of the p-value used to conduct this test?
A) p-value lies between 0.005 and 0.010
B) p-value lies between 0.010 and 0.025
C) p-value lies between 0.050 and 0.10
D) p-value lies between 0.025 and 0.05
A) p-value lies between 0.005 and 0.010
B) p-value lies between 0.010 and 0.025
C) p-value lies between 0.050 and 0.10
D) p-value lies between 0.025 and 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
55
We conduct the following hypothesis test H0: σ2 = 82, HA: σ2 ≠ 82. For a random sample of 15 observations, the sample standard deviation is 12. Which of the following is the correct approximation of the p-value used to conduct this test?
A) p-value lies between 0.025 and 0.05
B) p-value lies between 0.01 and 0.025
C) p-value lies between 0.05 and 0.10
D) p-value is greater than 0.10
A) p-value lies between 0.025 and 0.05
B) p-value lies between 0.01 and 0.025
C) p-value lies between 0.05 and 0.10
D) p-value is greater than 0.10

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
56
Which of the following is the formula for a confidence interval for the ratio of the population variances 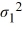 /
/ 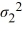 ?
?
A)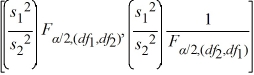
B)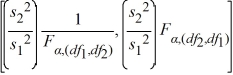
C)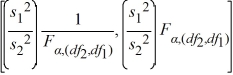
D)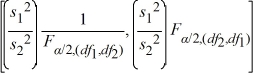
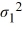 /
/ 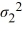 ?
?A)
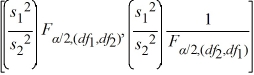
B)
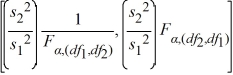
C)
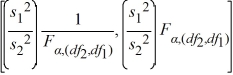
D)
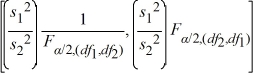

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
57
Becky owns a diner and is concerned about sustaining the business. She wants to ascertain if the standard deviation of the profits for each week is greater than $250. The details of the profits for the week are (in dollars) 1,743 1,438 1,212 1,705 1,985 1,857 1,916
Assume that profits are normally distributed. Which of the following is the correct value of the test statistic?
A) 6.146
B) 8.604
C) 6.652
D) 7.375
Assume that profits are normally distributed. Which of the following is the correct value of the test statistic?
A) 6.146
B) 8.604
C) 6.652
D) 7.375

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
58
Becky owns a diner and is concerned about sustaining the business. She wants to ascertain if the standard deviation of the profits for each week is greater than $250. The details of the profits for the week are (in dollars) 1,743 1,438 1,212 1,705 1,985 1,857 1,916
Assume that profits are normally distributed. Using the critical value approach at α = 0.05, which of the following is the correct conclusion for Becky's concern?
A) We reject H0 because the value of the test statistic is greater than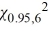 = 1.635.
= 1.635.
B) We do not reject H0 because the value of the test statistic is greater than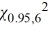 = 1.635.
= 1.635.
C) We reject H0 because the value of the test statistic is less than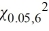 = 12.592.
= 12.592.
D) We do not reject H0 because the value of the test statistic is less than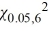 = 12.592.
= 12.592.
Assume that profits are normally distributed. Using the critical value approach at α = 0.05, which of the following is the correct conclusion for Becky's concern?
A) We reject H0 because the value of the test statistic is greater than
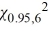 = 1.635.
= 1.635.B) We do not reject H0 because the value of the test statistic is greater than
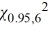 = 1.635.
= 1.635.C) We reject H0 because the value of the test statistic is less than
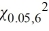 = 12.592.
= 12.592.D) We do not reject H0 because the value of the test statistic is less than
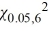 = 12.592.
= 12.592.
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
59
Which of the following is the value of x for which P 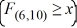 = 0.025?
= 0.025?
A) 4.07
B) 5.46
C) 3.22
D) 5.39
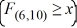 = 0.025?
= 0.025?A) 4.07
B) 5.46
C) 3.22
D) 5.39

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
60
Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n1 = 11 and n2 = 16 with sample variances of ![<strong>Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n<sub>1</sub> = 11 and n<sub>2</sub> = 16 with sample variances of and = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.</strong> A) [0.90, 2.41] B) [0.50, 2.00] C) [0.25, 4.00] D) [0.79, 5.70]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e3_634d_b223_61328aa1ba46_TB6618_11.jpg) and
and ![<strong>Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n<sub>1</sub> = 11 and n<sub>2</sub> = 16 with sample variances of and = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.</strong> A) [0.90, 2.41] B) [0.50, 2.00] C) [0.25, 4.00] D) [0.79, 5.70]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e3_8a5e_b223_1b6a8aa8c3e4_TB6618_11.jpg) = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.
= 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.
A) [0.90, 2.41]
B) [0.50, 2.00]
C) [0.25, 4.00]
D) [0.79, 5.70]
![<strong>Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n<sub>1</sub> = 11 and n<sub>2</sub> = 16 with sample variances of and = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.</strong> A) [0.90, 2.41] B) [0.50, 2.00] C) [0.25, 4.00] D) [0.79, 5.70]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e3_634d_b223_61328aa1ba46_TB6618_11.jpg) and
and ![<strong>Students of two sections of a history course took a common final examination. The course instructor examines the variance in scores between the two sections. He selects random samples of n<sub>1</sub> = 11 and n<sub>2</sub> = 16 with sample variances of and = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.</strong> A) [0.90, 2.41] B) [0.50, 2.00] C) [0.25, 4.00] D) [0.79, 5.70]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e3_8a5e_b223_1b6a8aa8c3e4_TB6618_11.jpg) = 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.
= 200, respectively. Assuming that the population distributions are normal, construct a 90% confidence interval for the ratio of the population variance.A) [0.90, 2.41]
B) [0.50, 2.00]
C) [0.25, 4.00]
D) [0.79, 5.70]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
61
Construct a 95% confidence interval for the ratios of two population variances. The random samples of n1= 9 and n2= 11 with sample variances of ![<strong>Construct a 95% confidence interval for the ratios of two population variances. The random samples of n<sub>1</sub>= 9 and n<sub>2</sub>= 11 with sample variances of = 500 and = 250, respectively. Assume that the samples were drawn from a normal population.</strong> A) [0.50, 2.00] B) [0.52, 8.60] C) [0.25, 1.41] D) [0.44, 4.30]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e9_cc1d_b223_3bd64a820c98_TB6618_11.jpg) = 500 and
= 500 and ![<strong>Construct a 95% confidence interval for the ratios of two population variances. The random samples of n<sub>1</sub>= 9 and n<sub>2</sub>= 11 with sample variances of = 500 and = 250, respectively. Assume that the samples were drawn from a normal population.</strong> A) [0.50, 2.00] B) [0.52, 8.60] C) [0.25, 1.41] D) [0.44, 4.30]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e9_f32e_b223_3fc892ab4617_TB6618_11.jpg) = 250, respectively. Assume that the samples were drawn from a normal population.
= 250, respectively. Assume that the samples were drawn from a normal population.
A) [0.50, 2.00]
B) [0.52, 8.60]
C) [0.25, 1.41]
D) [0.44, 4.30]
![<strong>Construct a 95% confidence interval for the ratios of two population variances. The random samples of n<sub>1</sub>= 9 and n<sub>2</sub>= 11 with sample variances of = 500 and = 250, respectively. Assume that the samples were drawn from a normal population.</strong> A) [0.50, 2.00] B) [0.52, 8.60] C) [0.25, 1.41] D) [0.44, 4.30]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e9_cc1d_b223_3bd64a820c98_TB6618_11.jpg) = 500 and
= 500 and ![<strong>Construct a 95% confidence interval for the ratios of two population variances. The random samples of n<sub>1</sub>= 9 and n<sub>2</sub>= 11 with sample variances of = 500 and = 250, respectively. Assume that the samples were drawn from a normal population.</strong> A) [0.50, 2.00] B) [0.52, 8.60] C) [0.25, 1.41] D) [0.44, 4.30]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8e9_f32e_b223_3fc892ab4617_TB6618_11.jpg) = 250, respectively. Assume that the samples were drawn from a normal population.
= 250, respectively. Assume that the samples were drawn from a normal population.A) [0.50, 2.00]
B) [0.52, 8.60]
C) [0.25, 1.41]
D) [0.44, 4.30]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
62
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. 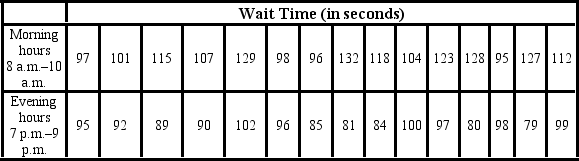 Which of the following is the correct approximation of the p-value?
Which of the following is the correct approximation of the p-value?
A) p-value is greater than 0.1.
B) p-value lies between 0.025 and 0.05.
C) p-value lies between 0.05 and 0.10.
D) p-value is greater than 0.2.
 Which of the following is the correct approximation of the p-value?
Which of the following is the correct approximation of the p-value?A) p-value is greater than 0.1.
B) p-value lies between 0.025 and 0.05.
C) p-value lies between 0.05 and 0.10.
D) p-value is greater than 0.2.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
63
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. 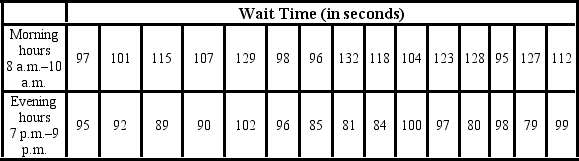 At the 10% significance level, which of the following is the correct conclusion?
At the 10% significance level, which of the following is the correct conclusion?
A) Do not reject H0. We cannot conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
B) Reject H0. We conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
C) Do not reject H0. We conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
D) Reject H0. We cannot conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
 At the 10% significance level, which of the following is the correct conclusion?
At the 10% significance level, which of the following is the correct conclusion?A) Do not reject H0. We cannot conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
B) Reject H0. We conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
C) Do not reject H0. We conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.
D) Reject H0. We cannot conclude that the variance of wait time during morning peak hours differs from that during the evening peak hours.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
64
A financial analyst examines the performance of two mutual funds and claims that the variances of the annual returns for the bond funds differ. To support his claim, he collects data on the annual returns (in percent) for the years 2001 through 2010. The analyst assumes that the annual returns for the two emerging market bond funds are normally distributed. Use the following summary statistics. 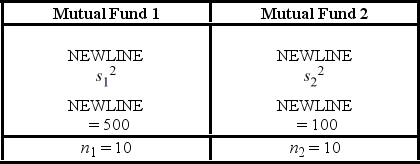 The competing hypotheses are Η0:
The competing hypotheses are Η0: 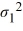 /
/ 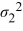 = 1, ΗA:
= 1, ΗA: 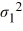 /
/ 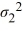 ≠ 1, At α = 0.10, is the analyst's claim supported by the data?
≠ 1, At α = 0.10, is the analyst's claim supported by the data?
A) No, the p-value < α = 0.10.
B) Yes, the p-value > α = 0.10.
C) No, the p-value > α = 0.10.
D) Yes, the p-value < α = 0.10.
 The competing hypotheses are Η0:
The competing hypotheses are Η0: 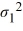 /
/ 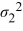 = 1, ΗA:
= 1, ΗA: 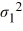 /
/ 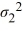 ≠ 1, At α = 0.10, is the analyst's claim supported by the data?
≠ 1, At α = 0.10, is the analyst's claim supported by the data?A) No, the p-value < α = 0.10.
B) Yes, the p-value > α = 0.10.
C) No, the p-value > α = 0.10.
D) Yes, the p-value < α = 0.10.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the expected returns (in percent) from the two investment options. Beth claims that the variances of the returns for the two investments differ. Use the following data to arrive at the results.  Which of the following is the correct p-value?
Which of the following is the correct p-value?
A) 0.2873
B) 0.7127
C) 0.3564
D) 0.6436
 Which of the following is the correct p-value?
Which of the following is the correct p-value?A) 0.2873
B) 0.7127
C) 0.3564
D) 0.6436

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
66
A financial analyst examines the performance of two mutual funds and claims that the variances of the annual returns for the bond funds differ. To support his claim, he collects data on the annual returns (in percent) for the years 2001 through 2010. The analyst assumes that the annual returns for the two emerging market bond funds are normally distributed. Use the following summary statistics. 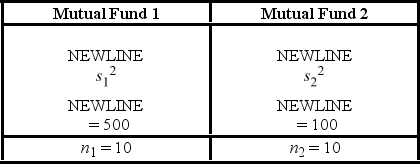 For the competing hypotheses Η0:
For the competing hypotheses Η0: 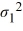 /
/ 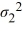 = 1, ΗA:
= 1, ΗA: 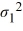 /
/ 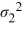 ≠ 1, which of the following is the correct approximation of the p-value?
≠ 1, which of the following is the correct approximation of the p-value?
A) Less than 0.01
B) Between 0.01 and 0.025
C) Between 0.02 and 0.05
D) Between 0.05 and 0.10
 For the competing hypotheses Η0:
For the competing hypotheses Η0: 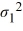 /
/ 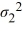 = 1, ΗA:
= 1, ΗA: 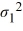 /
/ 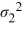 ≠ 1, which of the following is the correct approximation of the p-value?
≠ 1, which of the following is the correct approximation of the p-value?A) Less than 0.01
B) Between 0.01 and 0.025
C) Between 0.02 and 0.05
D) Between 0.05 and 0.10

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
67
The following are the competing hypotheses and the relevant summary statistics Η0: 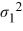 /
/ 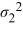 ≤ 1, ΗA:
≤ 1, ΗA: 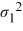 /
/ 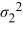 > 1.
> 1. 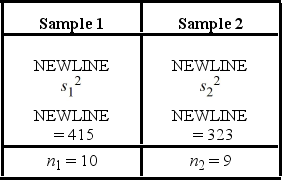 Which of the following statements is correct, regarding the assumptions for conducting the hypothesis test?
Which of the following statements is correct, regarding the assumptions for conducting the hypothesis test?
A) The samples are drawn from populations that are not normally distributed.
B) The values in one group are related to the values in the other group.
C) The difference of the sample variances is used to test the hypotheses.
D) The samples are independent and drawn from normally distributed populations.
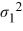 /
/ 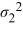 ≤ 1, ΗA:
≤ 1, ΗA: 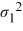 /
/ 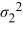 > 1.
> 1.  Which of the following statements is correct, regarding the assumptions for conducting the hypothesis test?
Which of the following statements is correct, regarding the assumptions for conducting the hypothesis test?A) The samples are drawn from populations that are not normally distributed.
B) The values in one group are related to the values in the other group.
C) The difference of the sample variances is used to test the hypotheses.
D) The samples are independent and drawn from normally distributed populations.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
68
The following are the competing hypotheses and the relevant summary statistics: Η0: 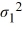 /
/ 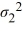 ≤ 1, ΗA:
≤ 1, ΗA: 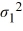 /
/ 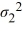 > 1.
> 1. 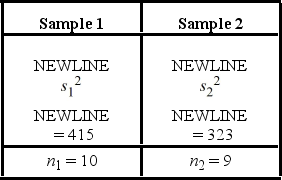 Which of the following is the critical value at the 5% significance level?
Which of the following is the critical value at the 5% significance level?
A) 3.02
B) 3.14
C) 3.23
D) 3.39
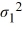 /
/ 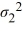 ≤ 1, ΗA:
≤ 1, ΗA: 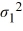 /
/ 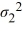 > 1.
> 1.  Which of the following is the critical value at the 5% significance level?
Which of the following is the critical value at the 5% significance level?A) 3.02
B) 3.14
C) 3.23
D) 3.39

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the expected returns (in percent) from the two investment options. Beth claims that the variances of the returns for the two investments differ. Use the following data to arrive at the results.  Test Beth's claim at the 5% significance level. Which of the following is the correct conclusion?
Test Beth's claim at the 5% significance level. Which of the following is the correct conclusion?
A) p-value = 0.7127 > α = 0.05; Beth's claim is correct.
B) p-value = 0.7127 > α = 0.05; Beth's claim is wrong.
C) p-value = 0.7127 < α = 0.05; Beth's claim is wrong.
D) p-value = 0.7127 < α = 0.05; Beth's claim is correct.
 Test Beth's claim at the 5% significance level. Which of the following is the correct conclusion?
Test Beth's claim at the 5% significance level. Which of the following is the correct conclusion?A) p-value = 0.7127 > α = 0.05; Beth's claim is correct.
B) p-value = 0.7127 > α = 0.05; Beth's claim is wrong.
C) p-value = 0.7127 < α = 0.05; Beth's claim is wrong.
D) p-value = 0.7127 < α = 0.05; Beth's claim is correct.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
70
The following are the competing hypotheses and the relevant summary statistics: Η0: 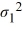 /
/ 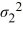 ≤ 1, ΗA:
≤ 1, ΗA: 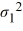 /
/ 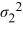 > 1.
> 1. 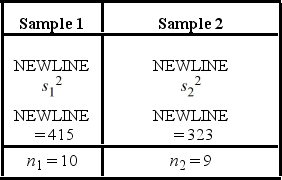 The p-value associated with the value of the test statistic is 0.3692. At the 5% significance level, which of the following conclusions is correct?
The p-value associated with the value of the test statistic is 0.3692. At the 5% significance level, which of the following conclusions is correct?
A) We reject the null hypothesis and conclude the first variance is larger than the second.
B) We do not reject the null hypothesis and conclude the first variance is larger than the second.
C) We reject the null hypothesis and cannot conclude the first variance is larger than the second.
D) We do not reject the null hypothesis and cannot conclude the first variance is larger than the second.
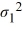 /
/ 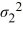 ≤ 1, ΗA:
≤ 1, ΗA: 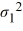 /
/ 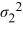 > 1.
> 1.  The p-value associated with the value of the test statistic is 0.3692. At the 5% significance level, which of the following conclusions is correct?
The p-value associated with the value of the test statistic is 0.3692. At the 5% significance level, which of the following conclusions is correct?A) We reject the null hypothesis and conclude the first variance is larger than the second.
B) We do not reject the null hypothesis and conclude the first variance is larger than the second.
C) We reject the null hypothesis and cannot conclude the first variance is larger than the second.
D) We do not reject the null hypothesis and cannot conclude the first variance is larger than the second.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the expected returns (in percent) from two investment options. Beth wants to determine if investment 1 has a lower variance. Use the following summary statistics.  Which of the following are the competing hypotheses for this test?
Which of the following are the competing hypotheses for this test?
A) Η0: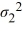 /
/ 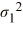 ≤ 1, ΗA:
≤ 1, ΗA: 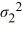 /
/ 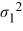 > 1
> 1
B) Η0: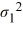 /
/ 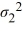 ≤ 1, ΗA:
≤ 1, ΗA: 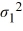 /
/ 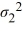 > 1
> 1
C) Η0: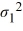 /
/ 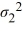 = 1, ΗA:
= 1, ΗA: 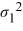 /
/ 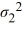 ≠ 1
≠ 1
D) Η0: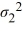 /
/ 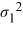 ≥ 1, ΗA:
≥ 1, ΗA: 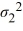 /
/ 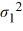 < 1
< 1
 Which of the following are the competing hypotheses for this test?
Which of the following are the competing hypotheses for this test?A) Η0:
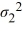 /
/ 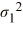 ≤ 1, ΗA:
≤ 1, ΗA: 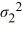 /
/ 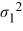 > 1
> 1B) Η0:
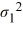 /
/ 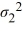 ≤ 1, ΗA:
≤ 1, ΗA: 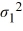 /
/ 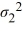 > 1
> 1C) Η0:
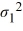 /
/ 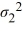 = 1, ΗA:
= 1, ΗA: 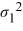 /
/ 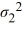 ≠ 1
≠ 1D) Η0:
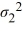 /
/ 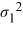 ≥ 1, ΗA:
≥ 1, ΗA: 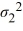 /
/ 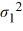 < 1
< 1
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
72
Which of the following Excel's functions is used to calculate the right-tailed probability for a value x on the 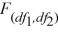 distribution?
distribution?
A) F.DIST.RT(x, Deg_freedom1, Deg_freedom2, Cumulative)
B) F.DIST.RT(x, n1, n2)
C) F.DIST.RT(x, n1−1, n2−2)
D) F.DIST.RT(x, Deg_freedom1, Deg_freedom2)
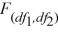 distribution?
distribution?A) F.DIST.RT(x, Deg_freedom1, Deg_freedom2, Cumulative)
B) F.DIST.RT(x, n1, n2)
C) F.DIST.RT(x, n1−1, n2−2)
D) F.DIST.RT(x, Deg_freedom1, Deg_freedom2)

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
73
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. ![<strong>Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?</strong> A) We cannot conclude the variance of the wait times for the morning hours is different from the variance of the wait times for the evening hours. B) We can conclude the variance of the wait times for the morning hours is more than the variance of the wait times for the evening hours. C) We can conclude the variance of the wait times for the evening hours is more than the variance of the wait times for the morning hours. D) We can conclude the variance of the wait times for the evening hours is equal to the the variance of the wait times for the morning hours.](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8ed_c3e2_b223_3906a2850759_TB6618_00.jpg) A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?
A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?
A) We cannot conclude the variance of the wait times for the morning hours is different from the variance of the wait times for the evening hours.
B) We can conclude the variance of the wait times for the morning hours is more than the variance of the wait times for the evening hours.
C) We can conclude the variance of the wait times for the evening hours is more than the variance of the wait times for the morning hours.
D) We can conclude the variance of the wait times for the evening hours is equal to the the variance of the wait times for the morning hours.
![<strong>Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?</strong> A) We cannot conclude the variance of the wait times for the morning hours is different from the variance of the wait times for the evening hours. B) We can conclude the variance of the wait times for the morning hours is more than the variance of the wait times for the evening hours. C) We can conclude the variance of the wait times for the evening hours is more than the variance of the wait times for the morning hours. D) We can conclude the variance of the wait times for the evening hours is equal to the the variance of the wait times for the morning hours.](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8ed_c3e2_b223_3906a2850759_TB6618_00.jpg) A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?
A 90% confidence interval is found to be [1.19, 7.36], where the morning is the first group and the evening is the second group. Which of the following is the correct conclusion?A) We cannot conclude the variance of the wait times for the morning hours is different from the variance of the wait times for the evening hours.
B) We can conclude the variance of the wait times for the morning hours is more than the variance of the wait times for the evening hours.
C) We can conclude the variance of the wait times for the evening hours is more than the variance of the wait times for the morning hours.
D) We can conclude the variance of the wait times for the evening hours is equal to the the variance of the wait times for the morning hours.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
74
A financial analyst examines the performance of two mutual funds and claims that the variances of the annual returns for the bond funds differ. To support his claim, he collects data on the annual returns (in percent) for the years 2001 through 2010. The analyst assumes that the annual returns for the two emerging market bond funds are normally distributed. Use the following summary statistics. 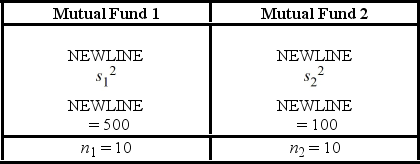 The competing hypotheses are Η0:
The competing hypotheses are Η0: 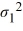 /
/ 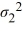 = 1, ΗA:
= 1, ΗA: 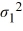 /
/ 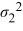 ≠ 1. At α = 0.10, is the analyst's claim supported by the data using the critical value approach?
≠ 1. At α = 0.10, is the analyst's claim supported by the data using the critical value approach?
A) No, because the value of the test statistic is less than the critical F value.
B) Yes, because the value of the test statistic is less than the critical F value.
C) Yes, because the value of the test statistic is greater than the critical F value.
D) No, because the value of the test statistic is greater than the critical F value.
 The competing hypotheses are Η0:
The competing hypotheses are Η0: 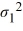 /
/ 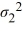 = 1, ΗA:
= 1, ΗA: 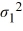 /
/ 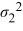 ≠ 1. At α = 0.10, is the analyst's claim supported by the data using the critical value approach?
≠ 1. At α = 0.10, is the analyst's claim supported by the data using the critical value approach?A) No, because the value of the test statistic is less than the critical F value.
B) Yes, because the value of the test statistic is less than the critical F value.
C) Yes, because the value of the test statistic is greater than the critical F value.
D) No, because the value of the test statistic is greater than the critical F value.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
75
The result of placing a larger sample variance in the numerator of the 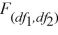 test statistic allows us to
test statistic allows us to
A) focus only on the right tail of the distribution.
B) arrive at a more accurate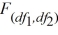 statistic value.
statistic value.
C) focus only on the left tail of the distribution.
D) determine if the distribution is symmetric.
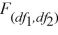 test statistic allows us to
test statistic allows us toA) focus only on the right tail of the distribution.
B) arrive at a more accurate
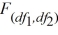 statistic value.
statistic value.C) focus only on the left tail of the distribution.
D) determine if the distribution is symmetric.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
76
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. 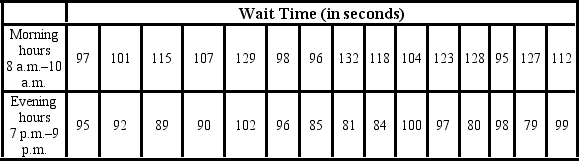 Which of the following is the correct value of the test statistic?
Which of the following is the correct value of the test statistic?
A) 1.72
B) 2.96
C) 1.66
D) 0.34
 Which of the following is the correct value of the test statistic?
Which of the following is the correct value of the test statistic?A) 1.72
B) 2.96
C) 1.66
D) 0.34

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
77
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. ![<strong>Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. Which of the following is the 95% confidence interval for the ratio of the population variances?</strong> A) [1.02, 8.55] B) [1.00, 8.73] C) [0.99, 8.83] D) [1.19, 7.34]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8ed_9cd1_b223_03177e5279e1_TB6618_00.jpg) Which of the following is the 95% confidence interval for the ratio of the population variances?
Which of the following is the 95% confidence interval for the ratio of the population variances?
A) [1.02, 8.55]
B) [1.00, 8.73]
C) [0.99, 8.83]
D) [1.19, 7.34]
![<strong>Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m. and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. Which of the following is the 95% confidence interval for the ratio of the population variances?</strong> A) [1.02, 8.55] B) [1.00, 8.73] C) [0.99, 8.83] D) [1.19, 7.34]](https://d2lvgg3v3hfg70.cloudfront.net/TB6618/11ea8309_a8ed_9cd1_b223_03177e5279e1_TB6618_00.jpg) Which of the following is the 95% confidence interval for the ratio of the population variances?
Which of the following is the 95% confidence interval for the ratio of the population variances?A) [1.02, 8.55]
B) [1.00, 8.73]
C) [0.99, 8.83]
D) [1.19, 7.34]

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
78
Amie Jackson, a manager at Sigma travel services, makes every effort to ensure that customers attempting to make online reservations do not have to wait too long to complete the reservation process. The travel website is open for reservations 24 hours a day, and Amie regularly checks the website for the waiting time to maintain consistency in service. She uses the following independently drawn samples of wait time during two peak hours, morning 8 a.m. to 10 a.m., and evening 7 p.m. to 9 p.m., for the analysis. Assume that wait times are normally distributed. 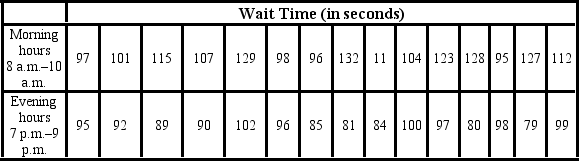 Which of the following is the correct hypotheses to determine if the variance of wait time during morning peak hours (population 1) differs from that during the evening peak hours (population 2)?
Which of the following is the correct hypotheses to determine if the variance of wait time during morning peak hours (population 1) differs from that during the evening peak hours (population 2)?
A) Η0: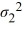 /
/ 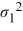 ≤ 1, ΗA:
≤ 1, ΗA: 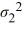 /
/ 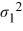 > 1
> 1
B) Η0: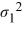 /
/ 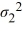 ≤ 1, ΗA:
≤ 1, ΗA: 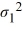 /
/ 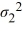 > 1
> 1
C) Η0: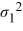 /
/ 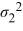 = 1, ΗA:
= 1, ΗA: 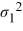 /
/ 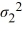 ≠ 1
≠ 1
D) Η0: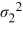 /
/ 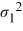 ≥ 1, ΗA:
≥ 1, ΗA: 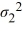 /
/ 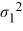 < 1
< 1
 Which of the following is the correct hypotheses to determine if the variance of wait time during morning peak hours (population 1) differs from that during the evening peak hours (population 2)?
Which of the following is the correct hypotheses to determine if the variance of wait time during morning peak hours (population 1) differs from that during the evening peak hours (population 2)?A) Η0:
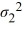 /
/ 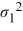 ≤ 1, ΗA:
≤ 1, ΗA: 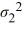 /
/ 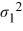 > 1
> 1B) Η0:
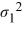 /
/ 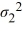 ≤ 1, ΗA:
≤ 1, ΗA: 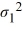 /
/ 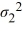 > 1
> 1C) Η0:
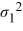 /
/ 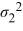 = 1, ΗA:
= 1, ΗA: 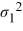 /
/ 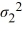 ≠ 1
≠ 1D) Η0:
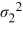 /
/ 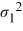 ≥ 1, ΗA:
≥ 1, ΗA: 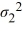 /
/ 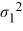 < 1
< 1
Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
79
Which of the following R functions is used to obtain a right-tail probability for a value x of the 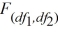 distribution?
distribution?
A) pf(x, df1, df2)
B) 1-pf(x, df1, df2)
C) pf(x, df2, df1)
D) 1-pf(x, df2, df1)
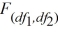 distribution?
distribution?A) pf(x, df1, df2)
B) 1-pf(x, df1, df2)
C) pf(x, df2, df1)
D) 1-pf(x, df2, df1)

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
80
A financial analyst examines the performance of two mutual funds and claims that the variances of the annual returns for the bond funds differ. To support his claim, he collects data on the annual returns (in percent) for the years 2001 through 2010. The analyst assumes that the annual returns for the two emerging market bond funds are normally distributed. Use the following summary statistics. 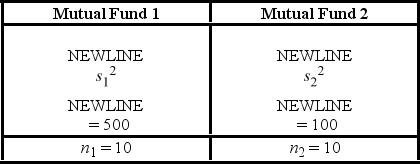 The competing hypotheses are Η0:
The competing hypotheses are Η0: 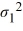 /
/ 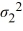 = 1, ΗA:
= 1, ΗA: 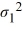 /
/ 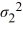 ≠ 1. Which of the following is the critical F value at the 10% significance level?
≠ 1. Which of the following is the critical F value at the 10% significance level?
A) F0.10,(9,9) = 2.44
B) F0.05,(10,10) = 2.98
C) F0.05,(9,9) = 3.18
D) F0.10,(10,10) = 2.32
 The competing hypotheses are Η0:
The competing hypotheses are Η0: 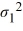 /
/ 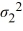 = 1, ΗA:
= 1, ΗA: 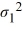 /
/ 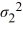 ≠ 1. Which of the following is the critical F value at the 10% significance level?
≠ 1. Which of the following is the critical F value at the 10% significance level?A) F0.10,(9,9) = 2.44
B) F0.05,(10,10) = 2.98
C) F0.05,(9,9) = 3.18
D) F0.10,(10,10) = 2.32

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck



