Deck 7: Linear Programming Under Uncertainty
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/7
Play
Full screen (f)
Deck 7: Linear Programming Under Uncertainty
1
Consider the following model.Minimize Z = c1x1 + c2x2,subject to a11x1 + a12x2 ≥ b1 a21x2 + a22x2 ≤ b2 and x1 ≥ 0,x2 ≥ 0.The estimates and ranges of uncertainty for the parameters are shown in the following table. 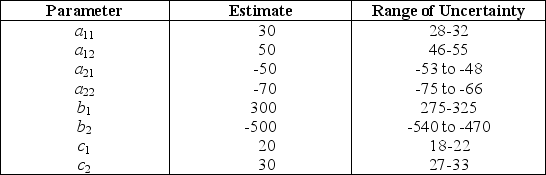 Use robust optimization to formulate a conservative version of this model.
Use robust optimization to formulate a conservative version of this model.
 Use robust optimization to formulate a conservative version of this model.
Use robust optimization to formulate a conservative version of this model.Robust optimization assigns the most conservative value to each parameter.Therefore,for the objective function in minimization form,it uses the maximum value of each cj.Since the first functional constraint is in ≥ form,it uses the minimum value of each a1j and the maximum value of b1.Since the second functional constraint is in ≤ form,it uses the maximum value of each a2j and the minimum value of b2.The resulting model is Minimize Z = 22x1 + 33x2,subject to 28x1 + 46x2 ≥ 325 -48x1 + -66x2 ≤ -540 and x1 ≥ 0,x2 ≥ 0.
2
Ken and Larry,Inc.,supplies its ice cream parlors with three flavors of ice cream: chocolate,vanilla,and banana.Due to extremely hot weather and a high demand for its products,the company has run short of its supply of ingredients: milk,sugar,and cream.Hence,they will not be able to fill all the orders received from their retail outlets,the ice cream parlors.Due to these circumstances,the company has decided to choose the amount of each flavor to produce that will maximize total profit,given the constraints on supply of the basic ingredients.The chocolate,vanilla,and banana flavors generate,respectively,$1.00,$0.90,and $0.95 of profit per gallon sold.The company has only 200 gallons of milk,150 pounds of sugar,and 60 gallons of cream left in its inventory.The linear programming formulation for this problem is shown below in algebraic form.Let C = gallons of chocolate ice cream produced,V = gallons of vanilla ice cream produced,B = gallons of banana ice cream produced.Maximize Profit = 1.00 C + 0.90 V + 0.95 B,subject to Milk: 0.45 C + 0.50 V + 0.40 B ≤ 200 gallons Sugar: 0.50 C + 0.40 V + 0.40 B ≤ 150 pounds Cream: 0.10 C + 0.15 V + 0.20 B ≤ 60 gallons and C ≥ 0,V ≥ 0,B ≥ 0.This problem was solved using the Excel Solver.The spreadsheet (already solve d)Suppose the company discovers that 3 gallons of cream have gone sour and so must be thrown out.Will the optimal solution change,and what can be said about the effect on total profit? (e)Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15.Should they? Explain.(f)Fill in all the sensitivity report information for the milk constraint,given just the optimal solution for the problem.Explain how you were able to deduce each number.d)and the sensitivity report are shown below.[Note: The numbers in the sensitivity report for the milk constraint are missing on purpose,since you will be asked to fill in these numbers in part (f).] ![Ken and Larry,Inc.,supplies its ice cream parlors with three flavors of ice cream: chocolate,vanilla,and banana.Due to extremely hot weather and a high demand for its products,the company has run short of its supply of ingredients: milk,sugar,and cream.Hence,they will not be able to fill all the orders received from their retail outlets,the ice cream parlors.Due to these circumstances,the company has decided to choose the amount of each flavor to produce that will maximize total profit,given the constraints on supply of the basic ingredients.The chocolate,vanilla,and banana flavors generate,respectively,$1.00,$0.90,and $0.95 of profit per gallon sold.The company has only 200 gallons of milk,150 pounds of sugar,and 60 gallons of cream left in its inventory.The linear programming formulation for this problem is shown below in algebraic form.Let C = gallons of chocolate ice cream produced,V = gallons of vanilla ice cream produced,B = gallons of banana ice cream produced.Maximize Profit = 1.00 C + 0.90 V + 0.95 B,subject to Milk: 0.45 C + 0.50 V + 0.40 B ≤ 200 gallons Sugar: 0.50 C + 0.40 V + 0.40 B ≤ 150 pounds Cream: 0.10 C + 0.15 V + 0.20 B ≤ 60 gallons and C ≥ 0,V ≥ 0,B ≥ 0.This problem was solved using the Excel Solver.The spreadsheet (already solve d)Suppose the company discovers that 3 gallons of cream have gone sour and so must be thrown out.Will the optimal solution change,and what can be said about the effect on total profit? (e)Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15.Should they? Explain.(f)Fill in all the sensitivity report information for the milk constraint,given just the optimal solution for the problem.Explain how you were able to deduce each number.d)and the sensitivity report are shown below.[Note: The numbers in the sensitivity report for the milk constraint are missing on purpose,since you will be asked to fill in these numbers in part (f).] For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c86c_8e71_83dc_8f89fb721873_TB2462_00.jpg) For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?
For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?
![Ken and Larry,Inc.,supplies its ice cream parlors with three flavors of ice cream: chocolate,vanilla,and banana.Due to extremely hot weather and a high demand for its products,the company has run short of its supply of ingredients: milk,sugar,and cream.Hence,they will not be able to fill all the orders received from their retail outlets,the ice cream parlors.Due to these circumstances,the company has decided to choose the amount of each flavor to produce that will maximize total profit,given the constraints on supply of the basic ingredients.The chocolate,vanilla,and banana flavors generate,respectively,$1.00,$0.90,and $0.95 of profit per gallon sold.The company has only 200 gallons of milk,150 pounds of sugar,and 60 gallons of cream left in its inventory.The linear programming formulation for this problem is shown below in algebraic form.Let C = gallons of chocolate ice cream produced,V = gallons of vanilla ice cream produced,B = gallons of banana ice cream produced.Maximize Profit = 1.00 C + 0.90 V + 0.95 B,subject to Milk: 0.45 C + 0.50 V + 0.40 B ≤ 200 gallons Sugar: 0.50 C + 0.40 V + 0.40 B ≤ 150 pounds Cream: 0.10 C + 0.15 V + 0.20 B ≤ 60 gallons and C ≥ 0,V ≥ 0,B ≥ 0.This problem was solved using the Excel Solver.The spreadsheet (already solve d)Suppose the company discovers that 3 gallons of cream have gone sour and so must be thrown out.Will the optimal solution change,and what can be said about the effect on total profit? (e)Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15.Should they? Explain.(f)Fill in all the sensitivity report information for the milk constraint,given just the optimal solution for the problem.Explain how you were able to deduce each number.d)and the sensitivity report are shown below.[Note: The numbers in the sensitivity report for the milk constraint are missing on purpose,since you will be asked to fill in these numbers in part (f).] For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c86c_8e71_83dc_8f89fb721873_TB2462_00.jpg) For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?
For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?(a)The optimal solution is to produce no chocolate ice cream,300 gallons of vanilla ice cream,and 75 gallons of banana ice cream.Total profit will be $341.25.(b)The optimal solution will change since $1.00 is outside the allowable range of $(0.95-0.05)to $(0.95 + 0.021429).The profit will go up,but how much can't be determined without re-solving.(c)The optimal solution will not change since $0.92 is within the allowable range.The total profit will decrease by (75)$0.03 = $2.25 to $339.(d)The optimal solution will change.Since the change is within the allowable range (the allowable decrease is 3.75),we can calculate the change in profit using the shadow price (1*3 = 3).The new profit will be $338.25.(e)This increase is outside of the allowable increase of 10,so the problem will have be re-solved to determine whether this is worthwhile.(f)The final value is 180 as shown in the totals column in the solution.The shadow price is 0 since we are using less milk than we have available.The right-hand side value is 200 as given in the problem.The allowable increase is infinity since we are already using less than is available.The allowable decrease is 20 since the solution will change once the right-hand side drops below 180.
3
Consider the following problem.Maximize Z = 3x1 + x2 + 2x3,subject to x1 - x2 + 2x3 ≤ 20 2x1 + x2 - x3 ≤ 10 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 and x5 denote the slack variables for the respective functional constraints.After we apply the simplex method,the final simplex tableau is 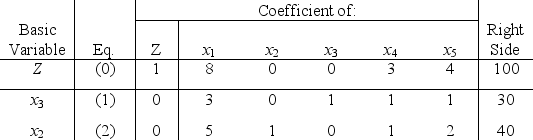
(a)Perform sensitivity analysis to determine which of the 11 parameters of the model are sensitive parameters in the sense that even small changes in just that parameter's value might change the optimal solution.
(b)Use algebraic analysis to find the allowable range to stay optimal for each cj..
(c)Use algebraic analysis to find the allowable range for each bi.

(a)Perform sensitivity analysis to determine which of the 11 parameters of the model are sensitive parameters in the sense that even small changes in just that parameter's value might change the optimal solution.
(b)Use algebraic analysis to find the allowable range to stay optimal for each cj..
(c)Use algebraic analysis to find the allowable range for each bi.
(a)If b1 or b2 is changed,then 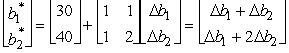 .So both b1 and b2 are sensitive parameters.If c1 changes,then the coefficient of x1 in Eq.(0)of the final tableau becomes
.So both b1 and b2 are sensitive parameters.If c1 changes,then the coefficient of x1 in Eq.(0)of the final tableau becomes 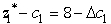 ,so the current optimal solution remains optimal as long as c1 ≤ 8.Since small changes in c1 will not affect the optimal solution,it is not a sensitive parameter.If either c2 or c3 changes,then the coefficient of x2 and x3 in Eq.(0)of the final tableau becomes 0 -
,so the current optimal solution remains optimal as long as c1 ≤ 8.Since small changes in c1 will not affect the optimal solution,it is not a sensitive parameter.If either c2 or c3 changes,then the coefficient of x2 and x3 in Eq.(0)of the final tableau becomes 0 - 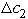 and 0 -
and 0 - 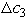 .Therefore,since x2 and x3 are basic variables,any change in
.Therefore,since x2 and x3 are basic variables,any change in 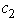 or
or 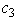 will require using elementary row operations to restore a value of 0 in the corresponding coefficient in the final tableau.However,since the coefficients of the nonbasic variables in Eq.(0)of the final tableau are rather large,a small change in either
will require using elementary row operations to restore a value of 0 in the corresponding coefficient in the final tableau.However,since the coefficients of the nonbasic variables in Eq.(0)of the final tableau are rather large,a small change in either 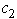 or
or 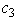 will not cause any of these coefficients of the nonbasic variables to become negative,so the current optimal solution would remain optimal.Consequently,
will not cause any of these coefficients of the nonbasic variables to become negative,so the current optimal solution would remain optimal.Consequently, 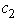 and
and 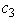 are not sensitive parameters.If a11 or a21 changes,it will only affect
are not sensitive parameters.If a11 or a21 changes,it will only affect 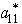 ,
, 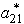 ,and
,and 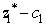 .The optimal solution will change only if the new value of
.The optimal solution will change only if the new value of 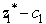 is negative.However,since the original value of
is negative.However,since the original value of 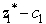 is such a large positive number (8),rather large changes in a11 or a21 would be needed to drive the value of
is such a large positive number (8),rather large changes in a11 or a21 would be needed to drive the value of 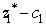 negative.So small changes will not affect the optimal solution.Hence,a11 and a21 are not sensitive parameters.Since x2 and x3 are basic variables,changes in a12,a13,a22,and a23 will require elementary row operations to restore proper form from Gaussian elimination.In the process,the entire row 1 and/or row 2,including the right-hand sides,will change.Therefore,the optimal solution will change.So these parameters are sensitive.(b)We have seen in part (a)that changes in c1 only affect the value of
negative.So small changes will not affect the optimal solution.Hence,a11 and a21 are not sensitive parameters.Since x2 and x3 are basic variables,changes in a12,a13,a22,and a23 will require elementary row operations to restore proper form from Gaussian elimination.In the process,the entire row 1 and/or row 2,including the right-hand sides,will change.Therefore,the optimal solution will change.So these parameters are sensitive.(b)We have seen in part (a)that changes in c1 only affect the value of 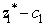 (the coefficient of x1 in Eq.(0)in the final tableau).If c1 = 3 changes to
(the coefficient of x1 in Eq.(0)in the final tableau).If c1 = 3 changes to 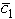 = 3 + c1,then
= 3 + c1,then 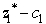 = 8 changes to
= 8 changes to 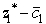 = 8 - c1.The current optimal solution remains optimal as long as
= 8 - c1.The current optimal solution remains optimal as long as 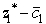 = 8 - ≥ 0,so c1 ≤ 8,so
= 8 - ≥ 0,so c1 ≤ 8,so 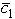 = 3 + c1 ≤ 11.Therefore,the allowable range to stay optimal for c1 is c1 11.For changes in c2,we noted in part (a)that the fact that x2 is a basic variable requires using elementary row operations to restore proper form from Gaussian elimination.In particular,if c2 changes by c2,then c2*Row 2 needs to be added to Row 0 to obtain the new Row 0 in proper form.Therefore,the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c2 * Row 2 0.This is equivalent to
= 3 + c1 ≤ 11.Therefore,the allowable range to stay optimal for c1 is c1 11.For changes in c2,we noted in part (a)that the fact that x2 is a basic variable requires using elementary row operations to restore proper form from Gaussian elimination.In particular,if c2 changes by c2,then c2*Row 2 needs to be added to Row 0 to obtain the new Row 0 in proper form.Therefore,the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c2 * Row 2 0.This is equivalent to 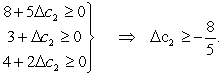 Since c2 = 1 + c2, the allowable range to stay optimal for c2 is c2 -3/5.For changes in c3,since x3 also is a basic variable,the same reasoning as for changes in c2 implies that the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c3 * Row 1 0.This is equivalent to
Since c2 = 1 + c2, the allowable range to stay optimal for c2 is c2 -3/5.For changes in c3,since x3 also is a basic variable,the same reasoning as for changes in c2 implies that the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c3 * Row 1 0.This is equivalent to 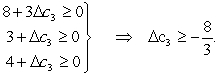 Since c3 = 2 + c3,the allowable range to stay optimal for c3 is c3 -2/3.
Since c3 = 2 + c3,the allowable range to stay optimal for c3 is c3 -2/3.
(c)Changes in the right-hand side only affect the final right-hand side b*.We require b* 0.For b1,we need b* + S*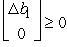 or,equivalently,
or,equivalently, 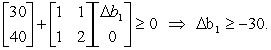 Since b1 = 20 + b1, the allowable range for b1 is b1 -10.For b2,we need b* + S*
Since b1 = 20 + b1, the allowable range for b1 is b1 -10.For b2,we need b* + S* 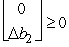 or,equivalently,
or,equivalently, 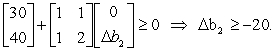 Since b2 = 10 + b2, the allowable range for b2 is b2 -10.
Since b2 = 10 + b2, the allowable range for b2 is b2 -10.
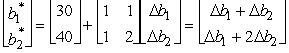 .So both b1 and b2 are sensitive parameters.If c1 changes,then the coefficient of x1 in Eq.(0)of the final tableau becomes
.So both b1 and b2 are sensitive parameters.If c1 changes,then the coefficient of x1 in Eq.(0)of the final tableau becomes 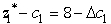 ,so the current optimal solution remains optimal as long as c1 ≤ 8.Since small changes in c1 will not affect the optimal solution,it is not a sensitive parameter.If either c2 or c3 changes,then the coefficient of x2 and x3 in Eq.(0)of the final tableau becomes 0 -
,so the current optimal solution remains optimal as long as c1 ≤ 8.Since small changes in c1 will not affect the optimal solution,it is not a sensitive parameter.If either c2 or c3 changes,then the coefficient of x2 and x3 in Eq.(0)of the final tableau becomes 0 - 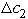 and 0 -
and 0 - 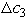 .Therefore,since x2 and x3 are basic variables,any change in
.Therefore,since x2 and x3 are basic variables,any change in 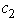 or
or 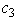 will require using elementary row operations to restore a value of 0 in the corresponding coefficient in the final tableau.However,since the coefficients of the nonbasic variables in Eq.(0)of the final tableau are rather large,a small change in either
will require using elementary row operations to restore a value of 0 in the corresponding coefficient in the final tableau.However,since the coefficients of the nonbasic variables in Eq.(0)of the final tableau are rather large,a small change in either 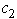 or
or 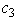 will not cause any of these coefficients of the nonbasic variables to become negative,so the current optimal solution would remain optimal.Consequently,
will not cause any of these coefficients of the nonbasic variables to become negative,so the current optimal solution would remain optimal.Consequently, 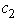 and
and 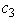 are not sensitive parameters.If a11 or a21 changes,it will only affect
are not sensitive parameters.If a11 or a21 changes,it will only affect 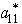 ,
, 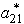 ,and
,and 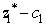 .The optimal solution will change only if the new value of
.The optimal solution will change only if the new value of 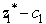 is negative.However,since the original value of
is negative.However,since the original value of 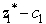 is such a large positive number (8),rather large changes in a11 or a21 would be needed to drive the value of
is such a large positive number (8),rather large changes in a11 or a21 would be needed to drive the value of 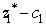 negative.So small changes will not affect the optimal solution.Hence,a11 and a21 are not sensitive parameters.Since x2 and x3 are basic variables,changes in a12,a13,a22,and a23 will require elementary row operations to restore proper form from Gaussian elimination.In the process,the entire row 1 and/or row 2,including the right-hand sides,will change.Therefore,the optimal solution will change.So these parameters are sensitive.(b)We have seen in part (a)that changes in c1 only affect the value of
negative.So small changes will not affect the optimal solution.Hence,a11 and a21 are not sensitive parameters.Since x2 and x3 are basic variables,changes in a12,a13,a22,and a23 will require elementary row operations to restore proper form from Gaussian elimination.In the process,the entire row 1 and/or row 2,including the right-hand sides,will change.Therefore,the optimal solution will change.So these parameters are sensitive.(b)We have seen in part (a)that changes in c1 only affect the value of 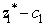 (the coefficient of x1 in Eq.(0)in the final tableau).If c1 = 3 changes to
(the coefficient of x1 in Eq.(0)in the final tableau).If c1 = 3 changes to 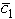 = 3 + c1,then
= 3 + c1,then 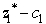 = 8 changes to
= 8 changes to 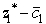 = 8 - c1.The current optimal solution remains optimal as long as
= 8 - c1.The current optimal solution remains optimal as long as 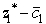 = 8 - ≥ 0,so c1 ≤ 8,so
= 8 - ≥ 0,so c1 ≤ 8,so 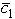 = 3 + c1 ≤ 11.Therefore,the allowable range to stay optimal for c1 is c1 11.For changes in c2,we noted in part (a)that the fact that x2 is a basic variable requires using elementary row operations to restore proper form from Gaussian elimination.In particular,if c2 changes by c2,then c2*Row 2 needs to be added to Row 0 to obtain the new Row 0 in proper form.Therefore,the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c2 * Row 2 0.This is equivalent to
= 3 + c1 ≤ 11.Therefore,the allowable range to stay optimal for c1 is c1 11.For changes in c2,we noted in part (a)that the fact that x2 is a basic variable requires using elementary row operations to restore proper form from Gaussian elimination.In particular,if c2 changes by c2,then c2*Row 2 needs to be added to Row 0 to obtain the new Row 0 in proper form.Therefore,the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c2 * Row 2 0.This is equivalent to 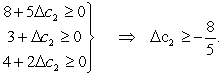 Since c2 = 1 + c2, the allowable range to stay optimal for c2 is c2 -3/5.For changes in c3,since x3 also is a basic variable,the same reasoning as for changes in c2 implies that the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c3 * Row 1 0.This is equivalent to
Since c2 = 1 + c2, the allowable range to stay optimal for c2 is c2 -3/5.For changes in c3,since x3 also is a basic variable,the same reasoning as for changes in c2 implies that the current optimal solution remains optimal (although the objective function value may change)if Row 0 + c3 * Row 1 0.This is equivalent to 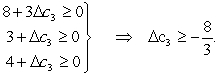 Since c3 = 2 + c3,the allowable range to stay optimal for c3 is c3 -2/3.
Since c3 = 2 + c3,the allowable range to stay optimal for c3 is c3 -2/3.(c)Changes in the right-hand side only affect the final right-hand side b*.We require b* 0.For b1,we need b* + S*
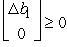 or,equivalently,
or,equivalently, 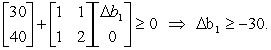 Since b1 = 20 + b1, the allowable range for b1 is b1 -10.For b2,we need b* + S*
Since b1 = 20 + b1, the allowable range for b1 is b1 -10.For b2,we need b* + S* 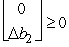 or,equivalently,
or,equivalently, 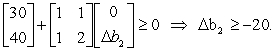 Since b2 = 10 + b2, the allowable range for b2 is b2 -10.
Since b2 = 10 + b2, the allowable range for b2 is b2 -10. 4
Consider the following problem.Maximize Z = 20x1 + c2x2,subject to 3x1 + a12x2 ≥ 60 5x2 + a22x2 ≤ 100 and x1 ≥ 0,x2 ≥ 0,where x1 represents the level of activity 1 and x2 represents the level of activity 2.The values of c2,a12,and a22 have not been determined yet.Only activity 1 needs to be undertaken soon whereas activity 2 will be initiated somewhat later.There are two different,but equally likely,scenarios that could unfold between now and the time activity 2 is undertaken that would lead to different values for c2,a12,and a22,as listed below.Scenario 1: c2 = 30,a12 = 4,and a22 = 7 Scenario 2: c2 = 10,a12 = 1,and a22 = 3 The goal is to use all of this information to choose a value for x1 now and to simultaneously determine a plan for choosing a value of x2 later after seeing which scenario has occurred.Use stochastic programming with recourse to formulate the appropriate model for this problem.

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
5
A certain linear programming problem has four functional constraints in inequality form such that their right-hand sides (the bi)are uncertain parameters.Therefore,chance constraints with = 0.95 have been introduced in place of these constraints.After next substituting the deterministic equivalents of these chance constraints and solving the resulting new linear programming model,its optimal solution is found to satisfy two of these deterministic equivalents with equality whereas there is some slack in the other two deterministic equivalents.Determine the lower bound and the upper bound on the probability that all of these four original constraints will turn out to be satisfied by the optimal solution for the new linear programming model so this solution actually will be feasible for the original problem.

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
6
Stickley Furniture is a manufacturer of fine hand-crafted furniture.During the next production period,management is considering producing dining room tables,dining room chairs,and/or bookcases.The time required for each item to go through the two stages of production (assembly and finishing),the amount of wood required (fine cherry wood)Suppose a worker in the assembly department calls in sick,so eight fewer hours now are available in the assembly department.How much would this affect total profit? Would it change the optimal production quantities? (e)Explain why the shadow price for the wood constraint is zero.(f)A new worker has been hired who is trained to do both assembly and finishing.She will split her time between the two areas,so there now are four additional hours available in both assembly and finishing.How much would this affect total profit? Would this change the optimal production quantities? (g)Based on the sensitivity report,is it wise to have the new worker in part f split her time equally between assembly and finishing,or would some other plan be better? (h)Use a parameter analysis report to determine how the optimal production quantities and total profit will change depending on how the new worker in part f allocates her time between assembly and finishing.In particular,assume 0,1,2,...,or 8 hours are added to assembly,with a corresponding 8,7,6,...,or 0 hours added to finishing.d),and the corresponding unit profits are given in the following table,along with the amount of each resource available in the upcoming production period. 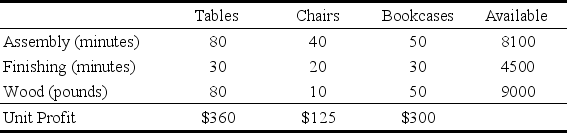 After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below.
After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below. 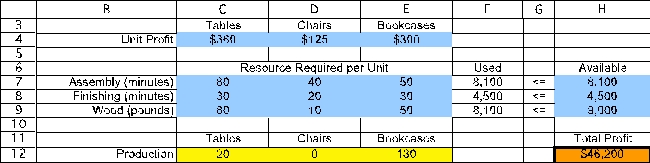
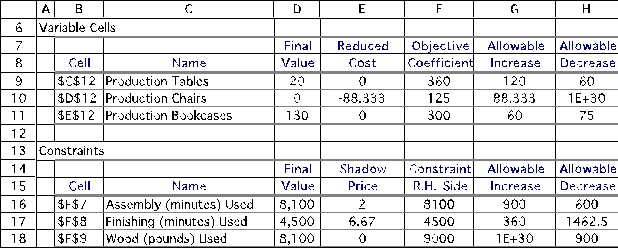 (a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit?
(a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit?
 After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below.
After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below. 
 (a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit?
(a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit?
Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the following problem.Maximize Z = 3x1 + 4x2 + 8x3,subject to 2x1 + 3x2 + 5x3 ≤ 9 x1 + 2x2 + 3x3 ≤ 5 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 and x5 denote the slack variables for the respective functional constraints.After we apply the simplex method,the final simplex tableau is 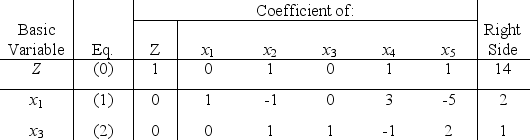 While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1
While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1
 While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1
While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1
Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck



