Deck 16: Regression Analysis: Model Building
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/82
Play
Full screen (f)
Deck 16: Regression Analysis: Model Building
1
The following regression model y = 0 + 1x1 + 2x2 +
Is known as
A)first-order model with one predictor variable
B)second-order model with two predictor variables
C)second-order model with one predictor variable
D)None of these alternatives is correct.
Is known as
A)first-order model with one predictor variable
B)second-order model with two predictor variables
C)second-order model with one predictor variable
D)None of these alternatives is correct.
second-order model with one predictor variable
2
A test to determine whether or not first-order autocorrelation is present is
A)a t test
B)the Durbin-Watson test
C)an F test
D)a chi-square test
A)a t test
B)the Durbin-Watson test
C)an F test
D)a chi-square test
B
3
The range of the Durbin-Watson statistic is between
A)-1 to 1
B)0 to 1
C)-infinity to + infinity
D)0 to 4
A)-1 to 1
B)0 to 1
C)-infinity to + infinity
D)0 to 4
D
4
In multiple regression analysis, the general linear model
A)cannot be used to accommodate curvilinear relationships between dependent variables and independent variables
B)can be used to accommodate curvilinear relationships between the independent variables and dependent variable
C)must contain more than 2 independent variables
D)None of these alternatives is correct.
A)cannot be used to accommodate curvilinear relationships between dependent variables and independent variables
B)can be used to accommodate curvilinear relationships between the independent variables and dependent variable
C)must contain more than 2 independent variables
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
5
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.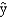 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x1
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
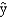 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x1
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following tests is used to determine whether an additional variable makes a significant contribution to a multiple regression model?
A)a t test
B)a Z test
C)an F test
D)a chi-square test
A)a t test
B)a Z test
C)an F test
D)a chi-square test

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
7
The correlation in error terms that arises when the error terms at successive points in time are related is termed
A)leverage
B)multicorrelation
C)autocorrelation
D)parallel correlation
A)leverage
B)multicorrelation
C)autocorrelation
D)parallel correlation

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
8
The joint effect of two variables acting together is called
A)autocorrelation
B)interaction
C)serial correlation
D)joint regression
A)autocorrelation
B)interaction
C)serial correlation
D)joint regression

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
9
The following model y = 0 + 1x1 +
Is referred to as a
A)curvilinear model
B)curvilinear model with one predictor variable
C)simple second-order model with one predictor variable
D)simple first-order model with one predictor variable
Is referred to as a
A)curvilinear model
B)curvilinear model with one predictor variable
C)simple second-order model with one predictor variable
D)simple first-order model with one predictor variable

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
10
A variable such as z, whose value is z = x1x2 is added to a general linear model in order to account for potential effects of two variables x1 and x2 acting together. This type of effect is
A)impossible to occur
B)called interaction
C)called multicollinearity effect
D)called transformation effect
A)impossible to occur
B)called interaction
C)called multicollinearity effect
D)called transformation effect

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
11
The parameters of nonlinear models have exponents
A)larger than zero
B)other than 1
C)only equal to 2
D)larger than 3
A)larger than zero
B)other than 1
C)only equal to 2
D)larger than 3

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
12
What value of Durbin-Watson statistic indicates no autocorrelation is present?
A)1
B)2
C)-2
D)0
A)1
B)2
C)-2
D)0

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
13
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.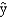 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model) the critical value of F at = 0.05 is
A)2.76
B)2.78
C)3.10
D)3.07
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
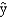 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model) the critical value of F at = 0.05 is
A)2.76
B)2.78
C)3.10
D)3.07

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
14
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.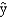 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The multiple coefficient of determination is
A)0.27
B)0.73
C)0.50
D)0.33
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
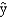 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The multiple coefficient of determination is
A)0.27
B)0.73
C)0.50
D)0.33

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
15
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.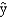 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x2
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
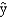 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x2
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
16
All the variables in a multiple regression analysis
A)must be quantitative
B)must be either quantitative or qualitative but not a mix of both
C)must be positive
D)None of these alternatives is correct.
A)must be quantitative
B)must be either quantitative or qualitative but not a mix of both
C)must be positive
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
17
In multiple regression analysis, the word "linear" in the term "general linear model" refers to the fact that
A) 0, 1, . . . p, all have exponents of 0
B) 0, 1, . . . p, all have exponents of 1
C) 0, 1, . . . p, all have exponents of at least 1
D) 0, 1, . . . p, all have exponents of less than 1
A) 0, 1, . . . p, all have exponents of 0
B) 0, 1, . . . p, all have exponents of 1
C) 0, 1, . . . p, all have exponents of at least 1
D) 0, 1, . . . p, all have exponents of less than 1

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
18
Serial correlation is
A)the correlation between serial numbers of products
B)the same as autocorrelation
C)the same as leverage
D)None of these alternatives is correct.
A)the correlation between serial numbers of products
B)the same as autocorrelation
C)the same as leverage
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
19
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.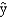 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x3
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
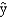 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The coefficient of x3
A)is significant
B)is not significant
C)cannot be tested, because not enough information is provided
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
20
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.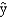 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. If you want to determine whether or not the coefficients of the independent variables are significant, the critical value of t statistic at = 0.05 is
A)2.080
B)2.060
C)2.064
D)1.96
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
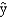 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. If you want to determine whether or not the coefficients of the independent variables are significant, the critical value of t statistic at = 0.05 is
A)2.080
B)2.060
C)2.064
D)1.96

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
21
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.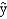 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The coefficient of determination for this model is
A)0.6923
B)0.1494
C)0.1300
D)0.8700
In a regression model involving 30 observations, the following estimated regression equation was obtained.
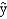 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The coefficient of determination for this model is
A)0.6923
B)0.1494
C)0.1300
D)0.8700

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
22
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.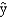 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The test statistic for testing the significance of the model is
A)0.730
B)18.926
C)3.703
D)1.369
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
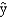 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The test statistic for testing the significance of the model is
A)0.730
B)18.926
C)3.703
D)1.369

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
23
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.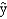 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The degrees of freedom associated with SSR are
A)3
B)33
C)32
D)30
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
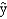 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The degrees of freedom associated with SSR are
A)3
B)33
C)32
D)30

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
24
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.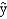 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SST are
A)24
B)6
C)19
D)None of these alternatives is correct.
In a regression model involving 30 observations, the following estimated regression equation was obtained.
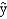 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SST are
A)24
B)6
C)19
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
25
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.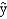 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The computed F value for testing the significance of the above model is
A)32.12
B)6.69
C)4.8
D)58
In a regression model involving 30 observations, the following estimated regression equation was obtained.
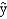 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The computed F value for testing the significance of the above model is
A)32.12
B)6.69
C)4.8
D)58

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
26
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.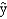 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The multiple coefficient of determination is
A)0.2
B)0.5
C)0.333
D)5
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
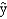 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The multiple coefficient of determination is
A)0.2
B)0.5
C)0.333
D)5

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
27
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.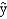 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of MSE is
A)348
B)10.40
C)10.83
D)32.13
In a regression model involving 30 observations, the following estimated regression equation was obtained.
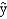 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of MSE is
A)348
B)10.40
C)10.83
D)32.13

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.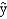 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SSE are
A)24
B)6
C)19
D)5
In a regression model involving 30 observations, the following estimated regression equation was obtained.
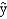 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SSE are
A)24
B)6
C)19
D)5

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
29
Exhibit 16-3
Below you are given a partial Excel output based on a sample of 25 observations.
-Refer to Exhibit 16-3. The estimated regression equation is
A)y = 0 + 1x1 + 2x2 + 3x3 +
B)E(y) = 0 + 1x1 + 2x2 + 3x3
C)= 29 + 5x1 + 6x2 + 4x3
D)= 145 + 20x1 - 18x2 + 4x3
E)None of the above answers are correct.
Below you are given a partial Excel output based on a sample of 25 observations.

-Refer to Exhibit 16-3. The estimated regression equation is
A)y = 0 + 1x1 + 2x2 + 3x3 +
B)E(y) = 0 + 1x1 + 2x2 + 3x3
C)= 29 + 5x1 + 6x2 + 4x3
D)= 145 + 20x1 - 18x2 + 4x3
E)None of the above answers are correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.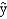 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of SSE is
A)3,740
B)170
C)260
D)2000
In a regression model involving 30 observations, the following estimated regression equation was obtained.
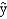 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of SSE is
A)3,740
B)170
C)260
D)2000

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
31
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.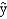 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of MSR is
A)10.40
B)348
C)10.83
D)52
In a regression model involving 30 observations, the following estimated regression equation was obtained.
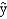 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The value of MSR is
A)10.40
B)348
C)10.83
D)52

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
32
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.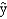 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was not given any protein and that did not take agent x2 is
A)36.7
B)34.3
C)36
D)38.4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
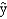 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was not given any protein and that did not take agent x2 is
A)36.7
B)34.3
C)36
D)38.4

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
33
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.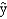 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. From the above function, it can be said that the life expectancy of rats that were given agent x2 is
A)1.7 months more than those who did not take agent x2
B)1.7 months less than those who did not take agent x2
C)0.8 months less than those who did not take agent x2
D)0.8 months more than those who did not take agent x2
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
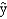 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. From the above function, it can be said that the life expectancy of rats that were given agent x2 is
A)1.7 months more than those who did not take agent x2
B)1.7 months less than those who did not take agent x2
C)0.8 months less than those who did not take agent x2
D)0.8 months more than those who did not take agent x2

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
34
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.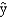 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
When dealing with the problem of non-constant variance, the reciprocal transformation means using
A)1/x as the independent variable instead of x
B)x2 as the independent variable instead of x
C)y2 as the dependent variable instead of y
D)1/y as the dependent variable instead of y
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
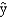 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
When dealing with the problem of non-constant variance, the reciprocal transformation means using
A)1/x as the independent variable instead of x
B)x2 as the independent variable instead of x
C)y2 as the dependent variable instead of y
D)1/y as the dependent variable instead of y

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
35
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.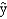 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was given 3 units of protein daily, and who took agent x2 is
A)36.7
B)36
C)49
D)38.4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
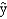 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was given 3 units of protein daily, and who took agent x2 is
A)36.7
B)36
C)49
D)38.4

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
36
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.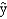 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The degrees of freedom associated with SSE are
A)3
B)33
C)32
D)30
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
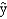 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The degrees of freedom associated with SSE are
A)3
B)33
C)32
D)30

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 16-3
Below you are given a partial Excel output based on a sample of 25 observations.
Refer to Exhibit 16-3. The critical t value obtained from the table to test an individual parameter at the 5% level is
A)2.06
B)2.069
C)2.074
D)2.080
Below you are given a partial Excel output based on a sample of 25 observations.

Refer to Exhibit 16-3. The critical t value obtained from the table to test an individual parameter at the 5% level is
A)2.06
B)2.069
C)2.074
D)2.080

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 16-2
In a regression model involving 30 observations, the following estimated regression equation was obtained.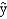 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SSR are
A)24
B)6
C)19
D)5
In a regression model involving 30 observations, the following estimated regression equation was obtained.
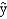 = 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5
= 170 + 34x1 - 3x2 + 8x3 + 58x4 + 3x5For this model, SSR = 1,740 and SST = 2,000.
Refer to Exhibit 16-2. The degrees of freedom associated with SSR are
A)24
B)6
C)19
D)5

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
39
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed.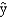 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The model
A)is significant
B)is not significant
C)may or may not be significant
D)None of these alternatives is correct.
In a regression analysis involving 25 observations, the following estimated regression equation was developed.
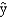 = 10 - 18x1 + 3x2 + 14x3
= 10 - 18x1 + 3x2 + 14x3Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
Refer to Exhibit 16-1. The model
A)is significant
B)is not significant
C)may or may not be significant
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
40
Exhibit 16-3
Below you are given a partial Excel output based on a sample of 25 observations.
-Refer to Exhibit 16-3. We want to test whether the parameter 2 is significant. The test statistic equals
A)4
B)5
C)3
D)-3
Below you are given a partial Excel output based on a sample of 25 observations.

-Refer to Exhibit 16-3. We want to test whether the parameter 2 is significant. The test statistic equals
A)4
B)5
C)3
D)-3

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
41
Excel's Regression tool can be used to perform the ____ procedure.
A)stepwise regression
B)forward selection
C)backward elimination
D)best-subsets
A)stepwise regression
B)forward selection
C)backward elimination
D)best-subsets

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
42
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.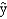 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was given 2 units of agent x2 daily, but was not given any protein is
A)32.6
B)36
C)38
D)34.3
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
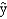 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The life expectancy of a rat that was given 2 units of agent x2 daily, but was not given any protein is
A)32.6
B)36
C)38
D)34.3

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.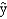 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. If we want to test for the significance of the model, the critical value of F at 95% confidence is
A)8.62
B)3.35
C)2.92
D)2.96
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
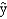 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. If we want to test for the significance of the model, the critical value of F at 95% confidence is
A)8.62
B)3.35
C)2.92
D)2.96

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
44
A regression model relating a dependent variable, y, with one independent variable, x1, resulted in an SSE of 400. Another regression model with the same dependent variable, y, and two independent variables, x1 and x2, resulted in an SSE of 320. At = .05, determine if x2 contributed significantly to the model. The sample size for both models was 20.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following statements about the backward elimination procedure is false?
A)It is a one-variable-at-a-time procedure.
B)It begins with the regression model found using the forward selection procedure.
C)It does not permit an independent variable to be reentered once it has been removed.
D)It does not guarantee that the best regression model will be found.
A)It is a one-variable-at-a-time procedure.
B)It begins with the regression model found using the forward selection procedure.
C)It does not permit an independent variable to be reentered once it has been removed.
D)It does not guarantee that the best regression model will be found.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
46
The forward selection procedure starts with how many independent variable(s) in the multiple regression model?
A)none
B)one
C)two
D)all of them
A)none
B)one
C)two
D)all of them

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
47
We want to test whether or not the addition of 3 variables to a model will be statistically significant. You are given the following information based on a sample of 25 observations. 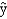 = 62.42 - 1.836x1 + 25.62x2
= 62.42 - 1.836x1 + 25.62x2
SSE = 725 SSR = 526
The equation was also estimated including the 3 variables. The results are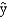 = 59.23 - 1.762x1 + 25.638x2 + 16.237x3 + 15.297x4 - 18.723x5
= 59.23 - 1.762x1 + 25.638x2 + 16.237x3 + 15.297x4 - 18.723x5
SSE = 520 SSR = 731
a.State the null and alternative hypotheses.
b.Test the null hypothesis at the 5% level of significance.
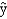 = 62.42 - 1.836x1 + 25.62x2
= 62.42 - 1.836x1 + 25.62x2SSE = 725 SSR = 526
The equation was also estimated including the 3 variables. The results are
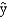 = 59.23 - 1.762x1 + 25.638x2 + 16.237x3 + 15.297x4 - 18.723x5
= 59.23 - 1.762x1 + 25.638x2 + 16.237x3 + 15.297x4 - 18.723x5SSE = 520 SSR = 731
a.State the null and alternative hypotheses.
b.Test the null hypothesis at the 5% level of significance.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
48
The variable selection procedure that identifies the best regression equation, given a specified number of independent variables, is
A)stepwise regression
B)forward selection
C)backward elimination
D)best-subsets regression
A)stepwise regression
B)forward selection
C)backward elimination
D)best-subsets regression

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
49
In a regression analysis involving 20 observations and five independent variables, the following information was obtained.  Fill in all the blanks in the above ANOVA table.
Fill in all the blanks in the above ANOVA table.
 Fill in all the blanks in the above ANOVA table.
Fill in all the blanks in the above ANOVA table.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
50
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.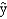 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The test statistic for testing the significance of the model is
A)0.50
B)5.00
C)0.25
D)0.33
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
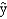 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The test statistic for testing the significance of the model is
A)0.50
B)5.00
C)0.25
D)0.33

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
51
When autocorrelation is present, one of the assumptions of the regression model is violated and that assumption is:
A)the expected value of the error term is zero
B)the variance of the error term is the same for all values of x
C)the values of the error term are independent
D)the values of the error term are normally distributed for all values of x
A)the expected value of the error term is zero
B)the variance of the error term is the same for all values of x
C)the values of the error term are independent
D)the values of the error term are normally distributed for all values of x

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.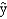 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The model
A)is significant
B)is not significant
C)Not enough information is provided to answer this question.
D)None of these alternatives is correct.
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed.
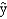 = 36 + 0.8x1 - 1.7x2
= 36 + 0.8x1 - 1.7x2Also provided are SSR = 60 and SST = 180.
Refer to Exhibit 16-4. The model
A)is significant
B)is not significant
C)Not enough information is provided to answer this question.
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
53
The null hypothesis in the Durbin-Watson test is always that there is
A)positive autocorrelation
B)negative autocorrelation
C)either positive or negative autocorrelation
D)no autocorrelation
A)positive autocorrelation
B)negative autocorrelation
C)either positive or negative autocorrelation
D)no autocorrelation

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
54
Multiple regression analysis was used to study the relationship between a dependent variable, y, and four independent variables; x1, x2, x3 and, x4. The following is a partial result of the regression analysis involving 31 observations. 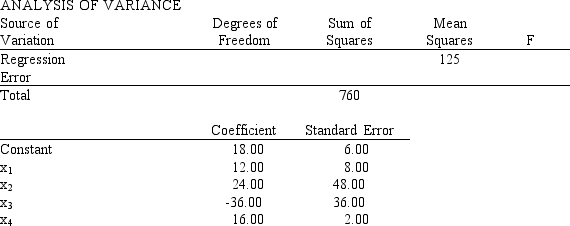
a.Compute the coefficient of determination.
b.At = 0.05, perform an F test and determine whether or not the regression model is significant.
c.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
d.Perform a t test and determine whether or not 4 is significantly different from zero ( = 0.05).

a.Compute the coefficient of determination.
b.At = 0.05, perform an F test and determine whether or not the regression model is significant.
c.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
d.Perform a t test and determine whether or not 4 is significantly different from zero ( = 0.05).

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
55
A regression model with one independent variable, x1, resulted in an SSE of 50. When a second independent variable, x2, was added to the model, the SSE was reduced to 40. At = 0.05, determine if x2 contributes significantly to the model. The sample size for both models was 30.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
56
A researcher is trying to decide whether or not to add another variable to his model. He has estimated the following model from a sample of 28 observations. 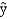 = 23.62 + 18.86x1 + 24.72x2
= 23.62 + 18.86x1 + 24.72x2
SSE = 1,425 SSR = 1,326
He has also estimated the model with an additional variable x3. The results are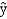 = 25.32 + 15.29x1 + 7.63x2 + 12.72x3
= 25.32 + 15.29x1 + 7.63x2 + 12.72x3
SSE = 1,300 SSR = 1,451
What advice would you give this researcher? Use a .05 level of significance.
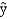 = 23.62 + 18.86x1 + 24.72x2
= 23.62 + 18.86x1 + 24.72x2SSE = 1,425 SSR = 1,326
He has also estimated the model with an additional variable x3. The results are
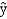 = 25.32 + 15.29x1 + 7.63x2 + 12.72x3
= 25.32 + 15.29x1 + 7.63x2 + 12.72x3SSE = 1,300 SSR = 1,451
What advice would you give this researcher? Use a .05 level of significance.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
57
Part of an Excel output relating y (dependent variable) and 4 independent variables, x1 through x4, is shown below. 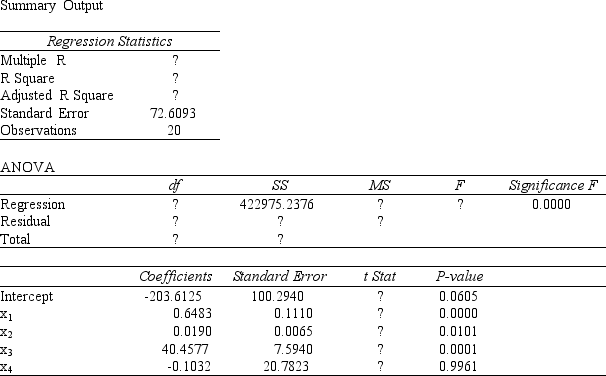
a.Fill in all the blanks marked with "?"
b.At a 5% significance level, which independent variables are significant and which ones are not? Fully explain how you arrived at your answers.

a.Fill in all the blanks marked with "?"
b.At a 5% significance level, which independent variables are significant and which ones are not? Fully explain how you arrived at your answers.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
58
Monthly total production costs and the number of units produced at a local company over a period of 10 months are shown below. 
a.Draw a scatter diagram for the above data.
b.Assume that a model in the form of
y = 0 + 1+
best describes the relationship between x and y. Estimate the parameters of this curvilinear regression equation.

a.Draw a scatter diagram for the above data.
b.Assume that a model in the form of
y = 0 + 1+
best describes the relationship between x and y. Estimate the parameters of this curvilinear regression equation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the following data. 
a.Draw a scatter diagram. Does the relationship between x and y appear to be linear?
b.Assume the relationship between x and y can best be given by
y = 0 + 1+
Estimate the parameters of this curvilinear function.

a.Draw a scatter diagram. Does the relationship between x and y appear to be linear?
b.Assume the relationship between x and y can best be given by
y = 0 + 1+
Estimate the parameters of this curvilinear function.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
60
Multiple regression analysis was used to study the relationship between a dependent variable, y, and three independent variables x1, x2 and, x3. The following is a partial result of the regression analysis involving 20 observations. 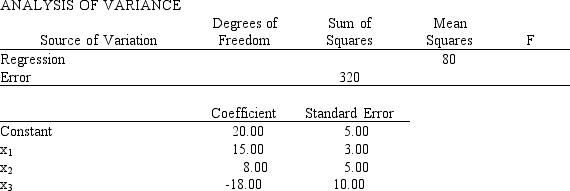
a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
c.Perform a t test and determine whether or not 2 is significantly different from zero ( = 0.05).
d.Perform a t test and determine whether or not 3 is significantly different from zero ( = 0.05).
e.At = 0.05, perform an F test and determine whether or not the regression model is significant.

a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not 1 is significantly different from zero ( = 0.05).
c.Perform a t test and determine whether or not 2 is significantly different from zero ( = 0.05).
d.Perform a t test and determine whether or not 3 is significantly different from zero ( = 0.05).
e.At = 0.05, perform an F test and determine whether or not the regression model is significant.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
61
A regression model relating the yearly income (y), age (x1), and the gender of the faculty member of a university (x2 = 1 if female and 0 if male) resulted in the following information. 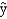 = 5,000 + 1.2x1 + 0.9x2
= 5,000 + 1.2x1 + 0.9x2
n = 20 SSE = 500 SSR = 1,500
Sb1 = 0.2 Sb2 = 0.1
a.Is gender a significant variable?
b.Determine the multiple coefficient of determination.
 = 5,000 + 1.2x1 + 0.9x2
= 5,000 + 1.2x1 + 0.9x2n = 20 SSE = 500 SSR = 1,500
Sb1 = 0.2 Sb2 = 0.1
a.Is gender a significant variable?
b.Determine the multiple coefficient of determination.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
62
Consider the following data. 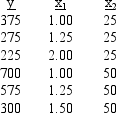 Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 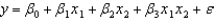
 Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 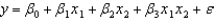

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
63
Monthly total production costs and the number of units produced at a local company over a period of 10 months are shown below.  Use Excel's Regression Tool to estimate a second-order model of the form
Use Excel's Regression Tool to estimate a second-order model of the form 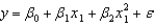
 Use Excel's Regression Tool to estimate a second-order model of the form
Use Excel's Regression Tool to estimate a second-order model of the form 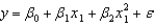

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
64
The following are partial results of a regression analysis involving sales (y in millions of dollars), advertising expenditures (x1 in thousands of dollars), and number of salespeople (x2) for a corporation. The regression was performed on a sample of 10 observations. 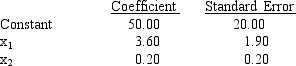
a.At = 0.05, test for the significance of the coefficient of advertising.
b.If the company uses $20,000 in advertisement and has 300 salespersons, what are the expected sales? (Give your answer in dollars.)

a.At = 0.05, test for the significance of the coefficient of advertising.
b.If the company uses $20,000 in advertisement and has 300 salespersons, what are the expected sales? (Give your answer in dollars.)

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the following data.  Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
 Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
66
A sample of 6 recent college graduates shows their current annual income (in $1000), years of education, and current age (in years). The data follow:  Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income.
Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income. 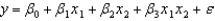
 Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income.
Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income. 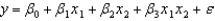

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
67
Thirty four observations of a dependent variable (y), and two independent variables resulted in an SSE of 300. When a third independent variable was added to the model, the SSE was reduced to 250. At a 5% level of significance, determine if the third independent variable contributes significantly to the model.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
68
When a regression model was developed relating sales (y) of a company to its product's price (x1), the SSE was determined to be 495. A second regression model relating sales (y) to product's price (x1) and competitor's product price (x2) resulted in an SSE of 396. At = 0.05, determine if the competitor's product's price contributed significantly to the model. The sample size for both models was 33.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
69
A regression analysis was applied in order to determine the relationship between a dependent variable and 4 independent variables. The following information was obtained from the regression analysis.R Square = 0.60
SSR = 4,800
Total number of observations n = 35
a.Fill in the blanks in the following ANOVA table.
b.At = 0.05 level of significance, test to determine if the model is significant.
SSR = 4,800
Total number of observations n = 35
a.Fill in the blanks in the following ANOVA table.
b.At = 0.05 level of significance, test to determine if the model is significant.


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
70
Forty-eight observations of a dependent variable (y) and five independent variables resulted in an SSE of 438. When two additional independent variables were added to the model, the SSE was reduced to 375. At a 5% level of significance, determine if the two additional independent variables contribute significantly to the model.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
71
In a regression analysis involving 18 observations and four independent variables, the following information was obtained.Multiple R = 0.6000
R Square = 0.3600
Standard Error = 4.8000
Based on the above information, fill in all the blanks in the following ANOVA table.
R Square = 0.3600
Standard Error = 4.8000
Based on the above information, fill in all the blanks in the following ANOVA table.


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
72
A regression analysis (involving 45 observations) relating a dependent variable (y) and two independent variables resulted in the following information. 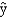 = 0.408 + 1.3387x1 + 2x2
= 0.408 + 1.3387x1 + 2x2
The SSE for the above model is 49.When two other independent variables were added to the model, the following information was provided.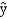 = 1.2 + 3.0x1 + 12x2 + 4.0x3 + 8x4
= 1.2 + 3.0x1 + 12x2 + 4.0x3 + 8x4
This latter model's SSE is 40.At a 5% significance level, test to determine if the two added independent variables contribute significantly to the model.
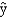 = 0.408 + 1.3387x1 + 2x2
= 0.408 + 1.3387x1 + 2x2The SSE for the above model is 49.When two other independent variables were added to the model, the following information was provided.
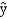 = 1.2 + 3.0x1 + 12x2 + 4.0x3 + 8x4
= 1.2 + 3.0x1 + 12x2 + 4.0x3 + 8x4This latter model's SSE is 40.At a 5% significance level, test to determine if the two added independent variables contribute significantly to the model.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the following data.  Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 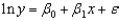
 Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 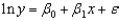

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
74
A regression analysis was applied in order to determine the relationship between a dependent variable and 14 independent variables. The following information was obtained from the regression analysis.R Square = 0.70
SSR = 7,000
Total number of observations n = 45
a.Fill in the blanks in the following ANOVA table.
b.At = 0.05 level of significance, test to determine if the model is significant.
SSR = 7,000
Total number of observations n = 45
a.Fill in the blanks in the following ANOVA table.
b.At = 0.05 level of significance, test to determine if the model is significant.


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the following data.  Use Excel's Regression Tool to estimate a second-order model of the form
Use Excel's Regression Tool to estimate a second-order model of the form 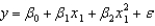
 Use Excel's Regression Tool to estimate a second-order model of the form
Use Excel's Regression Tool to estimate a second-order model of the form 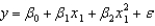

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
76
A regression analysis was applied in order to determine the relationship between a dependent variable and 8 independent variables. The following information was obtained from the regression analysis.R Square = 0.80
SSR = 4,280
Total number of observations n = 56
a.Fill in the blanks in the following ANOVA table.
b.Is the model significant? Let = 0.05.
SSR = 4,280
Total number of observations n = 56
a.Fill in the blanks in the following ANOVA table.
b.Is the model significant? Let = 0.05.


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the following data.  Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 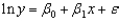
 Use Excel's Regression Tool to estimate a general linear model of the form
Use Excel's Regression Tool to estimate a general linear model of the form 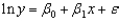

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the following data.  Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
 Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Use Excel's Regression Tool to estimate a general linear model that uses a reciprocal transformation on the dependent variable.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
79
A regression model relating units sold (y), price (x1), and whether or not promotion was used (x2 = 1 if promotion was used and 0 if it was not) resulted in the following model. 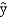 = 120 - 0.03x1 + 0.7x2
= 120 - 0.03x1 + 0.7x2
and the following information is provided.n = 15 Sb1 = .01 Sb2 = 0.1
a.Is price a significant variable?
b.Is promotion significant?
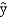 = 120 - 0.03x1 + 0.7x2
= 120 - 0.03x1 + 0.7x2and the following information is provided.n = 15 Sb1 = .01 Sb2 = 0.1
a.Is price a significant variable?
b.Is promotion significant?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
80
A soft drink manufacturer has developed a regression model relating sales (y in $10,000) with four independent variables. The four independent variables are price per unit (x1, in dollars), competitor's price (x2, in dollars), advertising (x3, in $1000) and type of container used (x4; 1 = Cans and 0 = Bottles). Part of the regression results are shown below. (Assume n = 25) 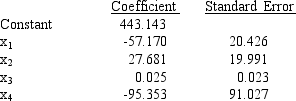
a.If the manufacturer uses can containers and if his price is $1.25, his advertising expenditure is $200,000, and his competitor's price is $1.50, what is your estimate of his sales? (Give your answer in dollars.)
b.Test to see if there is a significant relationship between sales and unit price. Let = 0.05.
c.Test to see if there is a significant relationship between sales and advertising. Let = 0.05.
d.Is the type of container a significant variable? Let = 0.05 = 0.05.
e.Test to see if there is a significant relationship between sales and competitor's price. Let = 0.05.

a.If the manufacturer uses can containers and if his price is $1.25, his advertising expenditure is $200,000, and his competitor's price is $1.50, what is your estimate of his sales? (Give your answer in dollars.)
b.Test to see if there is a significant relationship between sales and unit price. Let = 0.05.
c.Test to see if there is a significant relationship between sales and advertising. Let = 0.05.
d.Is the type of container a significant variable? Let = 0.05 = 0.05.
e.Test to see if there is a significant relationship between sales and competitor's price. Let = 0.05.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck



