Deck 8: Nonlinear Programming and Evolutionary Optimization
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/69
Play
Full screen (f)
Deck 8: Nonlinear Programming and Evolutionary Optimization
1
The optimal solution to a NLP problem can occur at an)
I)corner point.
II)interior point.
A)I is true
B)II is true
C)I and II are true
D)neither I or II is true
I)corner point.
II)interior point.
A)I is true
B)II is true
C)I and II are true
D)neither I or II is true
C
2
The Analytic Solver Platform solution strategy for NLP problems is the GRG method.What does GRG stand for?
A)Graphical Residual Gradient
B)Generalized Reduced Gradient
C)Goal Restricted Gradient
D)Gradually Reduced Gradient
A)Graphical Residual Gradient
B)Generalized Reduced Gradient
C)Goal Restricted Gradient
D)Gradually Reduced Gradient
B
3
What is the straight line Euclidean)distance between the points 5,7)and 1,11)?
A)2.83
B)5.65
C)8
D)16
A)2.83
B)5.65
C)8
D)16
B
4
When using the GRG algorithm to solve NLPs one should try multiple starting points because
A)If two different starting points return the same solution,that solution is optimal.
B)the solution returned depends upon the starting point.
C)the solution returned is always near the starting point.
D)a random element of GRG requires multiple starting points.
A)If two different starting points return the same solution,that solution is optimal.
B)the solution returned depends upon the starting point.
C)the solution returned is always near the starting point.
D)a random element of GRG requires multiple starting points.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is not an assumption of an EOQ problem.
A)Demand for a product is fairly constant.
B)Inventory depletion rates vary non-linearly.
C)Each new order is delivered in full when the inventory level reaches 0.
D)All are valid assumptions.
A)Demand for a product is fairly constant.
B)Inventory depletion rates vary non-linearly.
C)Each new order is delivered in full when the inventory level reaches 0.
D)All are valid assumptions.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
6
In a maximization problem,the GRG algorithm's search for a feasible direction of improvement equates to in the simplex algorithm for LP problems.
A)an adjacent corner point
B)a zero reduced cost
C)a positive shadow price
D)a positive reduced cost
A)an adjacent corner point
B)a zero reduced cost
C)a positive shadow price
D)a positive reduced cost

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
7
Which point or points are local optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 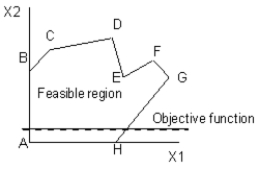
A)D
B)E
C)F
D)D,F

A)D
B)E
C)F
D)D,F

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
8
If the "Standard LP/Quadratic Engine" option is chosen in the Analytic Solver Platform ASP)task pane,ASP
A)will test for non-linearity in the model and apply GRG.
B)will test for non-linearity in the model and apply Simplex.
C)uses the B & B algorithm to solve the problem.
D)will apply Simplex if the linearity test passes.
A)will test for non-linearity in the model and apply GRG.
B)will test for non-linearity in the model and apply Simplex.
C)uses the B & B algorithm to solve the problem.
D)will apply Simplex if the linearity test passes.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
9
In NLP a local optimum is best described as
A)an interior point.
B)a corner point.
C)a point yielding no improving direction.
D)a good starting point for subsequent searches.
A)an interior point.
B)a corner point.
C)a point yielding no improving direction.
D)a good starting point for subsequent searches.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
10
Which point or points are global optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 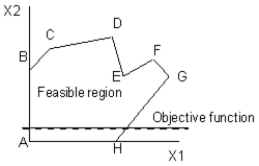
A)B
B)D
C)E
D)F

A)B
B)D
C)E
D)F

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
11
The GRG and Simplex algorithms are similar in that
A)each algorithm process continues until there is no further improvement in the objective function.
B)both algorithms take their starting solution from the spreadsheet.
C)both return the globally optimal solution.
D)both algorithms return a solution that satisfies at least one constraint at equality.
A)each algorithm process continues until there is no further improvement in the objective function.
B)both algorithms take their starting solution from the spreadsheet.
C)both return the globally optimal solution.
D)both algorithms return a solution that satisfies at least one constraint at equality.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
12
The GRG algorithm terminates when it
A)has completed 100 iterations.
B)has reached the global optimal solution.
C)when it detects no feasible direction for improvement.
D)when it reaches the steepest gradient.
A)has completed 100 iterations.
B)has reached the global optimal solution.
C)when it detects no feasible direction for improvement.
D)when it reaches the steepest gradient.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
13
The optimal trade-off between risk and return for a given portfolio problem can be summarized by the
A)efficient frontier.
B)investment frontier.
C)portfolio boundary.
D)variance boundary.
A)efficient frontier.
B)investment frontier.
C)portfolio boundary.
D)variance boundary.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
14
What is the search path for the following feasible solution space? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 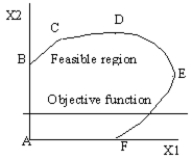
A)A,D
B)A,F,E,D
C)A,B,C,D
D)A,F,E

A)A,D
B)A,F,E,D
C)A,B,C,D
D)A,F,E

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
15
NLP problems which have slack in all the constraints
A)are infeasible.
B)are only at local optimal solutions.
C)have zeros for all shadow prices.
D)are at an interior point of the feasible region.
A)are infeasible.
B)are only at local optimal solutions.
C)have zeros for all shadow prices.
D)are at an interior point of the feasible region.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
16
The optimal solution to a LP problem is always at
I)a corner point.
II)an interior point
III)the origin.
A)I is true
B)II is true
C)III is true
D)I and III are true
I)a corner point.
II)an interior point
III)the origin.
A)I is true
B)II is true
C)III is true
D)I and III are true

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
17
In the GRG algorithm the initial solution is called the
A)originating point.
B)insertion point.
C)zero point.
D)starting point.
A)originating point.
B)insertion point.
C)zero point.
D)starting point.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
18
The main difference between LP and NLP problems is that NLPs will have a
A)linear objective function and nonlinear or linear constraints.
B)minimum of one nonlinear constraint or a nonlinear objective function.
C)multilevel objective functions.
D)multilevel objective function and nonlinear constraints.
A)linear objective function and nonlinear or linear constraints.
B)minimum of one nonlinear constraint or a nonlinear objective function.
C)multilevel objective functions.
D)multilevel objective function and nonlinear constraints.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
19
The GRG algorithm operates by
A)moving in the direction of most rapid improvement in the objective function.
B)choosing a search direction at random.
C)searching directly for the optimum solution.
D)moving in a clockwise direction.
A)moving in the direction of most rapid improvement in the objective function.
B)choosing a search direction at random.
C)searching directly for the optimum solution.
D)moving in a clockwise direction.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
20
The total annual cost for the economic order quantity model is
A)purchase cost + ordering cost + holding cost.
B)fixed ordering cost + holding cost.
C)purchase cost + fixed ordering cost.
D)unit cost + variable ordering cost + holding cost.
A)purchase cost + ordering cost + holding cost.
B)fixed ordering cost + holding cost.
C)purchase cost + fixed ordering cost.
D)unit cost + variable ordering cost + holding cost.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
21
A company has collected the following inventory data for an item.What is the total annual cost for this item?
Annual demand for the item D = 500
Unit purchase cost for the item C = 10
Fixed cost of placing an order S = 20
Cost of holding one unit in inventory for a year i = 30%
Order quantity Q = 50
A)275
B)450
C)5,275
D)5,450
Annual demand for the item D = 500
Unit purchase cost for the item C = 10
Fixed cost of placing an order S = 20
Cost of holding one unit in inventory for a year i = 30%
Order quantity Q = 50
A)275
B)450
C)5,275
D)5,450

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
22
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place
An order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What cell is the objective cell in this problem?
A)B3
B)B7
C)B9
D)B11
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place
An order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What cell is the objective cell in this problem?
A)B3
B)B7
C)B9
D)B11

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
23
How many local maximum solutions are there on this graph of a function? Mark their locations on the graph. 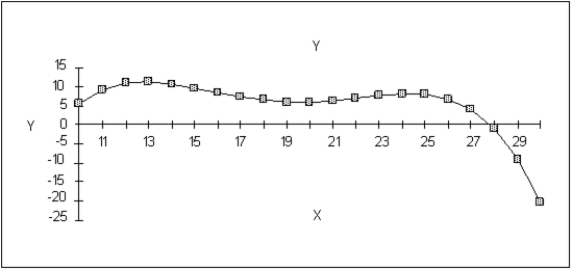


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
24
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell D12 of the spreadsheet for this problem?
A)=SUMPRODUCTB3:C3,B12:C12)
B)=SUMPRODUCTB4:C4,B12:C12)
C)=SUMPRODUCTB5:C5,B12:C12)
D)=SUMPRODUCTB7:C7,B12:C12)
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell D12 of the spreadsheet for this problem?
A)=SUMPRODUCTB3:C3,B12:C12)
B)=SUMPRODUCTB4:C4,B12:C12)
C)=SUMPRODUCTB5:C5,B12:C12)
D)=SUMPRODUCTB7:C7,B12:C12)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
25
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What cell is the variable cell in this problem?
A)B3
B)B7
C)B9
D)B11
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What cell is the variable cell in this problem?
A)B3
B)B7
C)B9
D)B11

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
26
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments.The problem is summarized in the accompanying spreadsheet.The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%,compounded quarterly,on his investments.He would like to know how low his annual return can be and still allow him to make his payments from interest income.What formula goes in cell C7 of the spreadsheet?
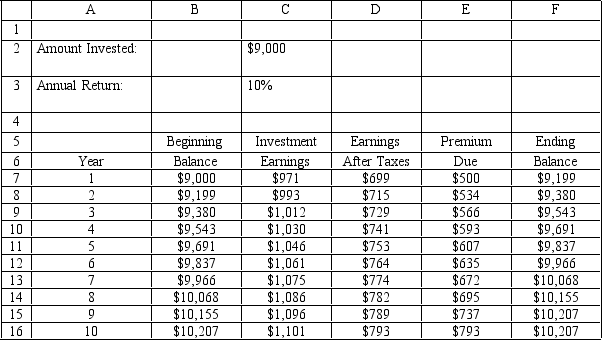
A)
B)
C)
D)
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments.The problem is summarized in the accompanying spreadsheet.The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%,compounded quarterly,on his investments.He would like to know how low his annual return can be and still allow him to make his payments from interest income.What formula goes in cell C7 of the spreadsheet?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
27
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell B7 of the spreadsheet for this problem?
A)= 30 ? .07 * C3
B)= 20 ? .1 * B3
C)= B3 ? B4
D)= B5 * B7 + C5 * C7
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell B7 of the spreadsheet for this problem?
A)= 30 ? .07 * C3
B)= 20 ? .1 * B3
C)= B3 ? B4
D)= B5 * B7 + C5 * C7

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-How much must the objective function coefficient of the variable Pumpkin change before any Pumpkins are
Produced based on the following sensitivity report?
Changing Cells
Final Reduced
Cell Name Value Gradient
$B$4 Corn 9.52 0
$C$4 Pumpkin 0 ?499.99
$D$4 Beans 10.79 0
Constraints
Final Lagrange
Cell Name Value Multiplier
$E$8 Corn 200000.00 0.016
$E$9 Pumpkin 99.00 12.000
$E$10 Beans 37777.78 0
$E$11 Water 29.84 0
$E$12 Fertilizer 8000.00 3.490
A)increase by 12
B)decrease by 12
C)increase by 499.99
D)decrease by 499.99
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-How much must the objective function coefficient of the variable Pumpkin change before any Pumpkins are
Produced based on the following sensitivity report?
Changing Cells
Final Reduced
Cell Name Value Gradient
$B$4 Corn 9.52 0
$C$4 Pumpkin 0 ?499.99
$D$4 Beans 10.79 0
Constraints
Final Lagrange
Cell Name Value Multiplier
$E$8 Corn 200000.00 0.016
$E$9 Pumpkin 99.00 12.000
$E$10 Beans 37777.78 0
$E$11 Water 29.84 0
$E$12 Fertilizer 8000.00 3.490
A)increase by 12
B)decrease by 12
C)increase by 499.99
D)decrease by 499.99

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
29
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-How much are additional units of Labor worth based on the following sensitivity report?
Changing Cells
Final Reduced
Cell Name Value Gradient
$B$4 Number to make: X1 9.42 0
$C$4 Number to make: X2 1.71 0
Constraints
Final Lagrange
Cell Name Value Multiplier
A)0
B)1.21
C)2.57
D)9.42
$D$8 Wood 42 0
$D$9 Labor 132 1.21
$D$10 Plywood 24 2.57
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-How much are additional units of Labor worth based on the following sensitivity report?
Changing Cells
Final Reduced
Cell Name Value Gradient
$B$4 Number to make: X1 9.42 0
$C$4 Number to make: X2 1.71 0
Constraints
Final Lagrange
Cell Name Value Multiplier
A)0
B)1.21
C)2.57
D)9.42
$D$8 Wood 42 0
$D$9 Labor 132 1.21
$D$10 Plywood 24 2.57

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.What formula goes in cell D9 of the spreadsheet?
A)=MIND4:D7)^2
B)=SUMD4:D7)
C)=SQRTD4^2+D5^2+D6^2+D7^2)
D)=SQRTMMULTB3:C3,D4:D7))
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.What formula goes in cell D9 of the spreadsheet?
A)=MIND4:D7)^2
B)=SUMD4:D7)
C)=SQRTD4^2+D5^2+D6^2+D7^2)
D)=SQRTMMULTB3:C3,D4:D7))

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
31
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.What formula goes in cell D4 of the spreadsheet?
A)=B4-$B$3)^2+C4-$C$3)^2
B)=SQRTB4-$B$3)+C4-$C$3))
C)=SQRTB4-$B$3)^2+C4-$C$3)^2)
D)=B4-$B$3)+C4-$C$3)
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.What formula goes in cell D4 of the spreadsheet?
A)=B4-$B$3)^2+C4-$C$3)^2
B)=SQRTB4-$B$3)+C4-$C$3))
C)=SQRTB4-$B$3)^2+C4-$C$3)^2)
D)=B4-$B$3)+C4-$C$3)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
32
The Reduced Gradient is similar to which of these terms from linear programming?
A)Shadow Price
B)Allowable Decrease
C)Allowable Increase
D)Reduced Cost
A)Shadow Price
B)Allowable Decrease
C)Allowable Increase
D)Reduced Cost

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
33
The Lagrange Multiplier is similar to which of these terms from linear programming?
A)Shadow Price
B)Allowable Increase
C)Allowable Decrease
D)Reduced Cost
A)Shadow Price
B)Allowable Increase
C)Allowable Decrease
D)Reduced Cost

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
34
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.Which cells)in the spreadsheet represent the decision variables in the problem?
A)B3
B)B3:C3
C)B4:C7
D)D9
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks.It has four stores and their coordinates are listed in the accompanying spreadsheet.Which cells)in the spreadsheet represent the decision variables in the problem?
A)B3
B)B3:C3
C)B4:C7
D)D9

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
35
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments.The problem is summarized in the accompanying spreadsheet.The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%,compounded quarterly,on his investments.He would like to know how low his annual return can be and still allow him to make his payments from interest income.What constraint must be entered in the Risk Solver Platform RSP)task pane?
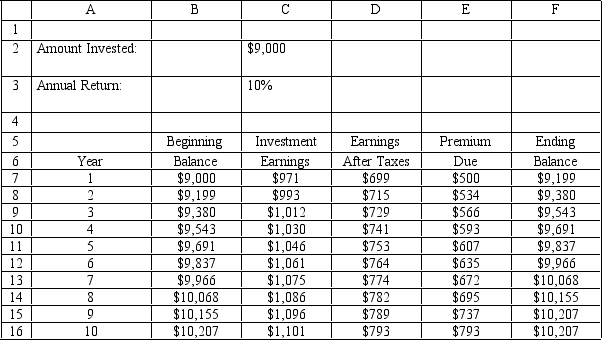
A)$D$7:$D$16 ? $E$7:$E$16
B)$C$7:$D$16 ? $E$7:$E$16.
C)$C$7:$C$16 ? $E$7:$E$16
D)$D$7:$D$16 ? $E$7:$E$16 .
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments.The problem is summarized in the accompanying spreadsheet.The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%,compounded quarterly,on his investments.He would like to know how low his annual return can be and still allow him to make his payments from interest income.What constraint must be entered in the Risk Solver Platform RSP)task pane?

A)$D$7:$D$16 ? $E$7:$E$16
B)$C$7:$D$16 ? $E$7:$E$16.
C)$C$7:$C$16 ? $E$7:$E$16
D)$D$7:$D$16 ? $E$7:$E$16 .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
36
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell B9 of the spreadsheet for this problem?
A)=B3*B7+C3*C7
B)=B5*B7+C5*C7
C)=B5-B4)*B7+C5-C4)*B7
D)=B3*B7+C3*B7+B4*B7+C4*B7
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-Refer to Exhibit 8.1.What formula is used in cell B9 of the spreadsheet for this problem?
A)=B3*B7+C3*C7
B)=B5*B7+C5*C7
C)=B5-B4)*B7+C5-C4)*B7
D)=B3*B7+C3*B7+B4*B7+C4*B7

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
37
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of product A costs 25 to make and demand is estimated to be 20 ?
)10 * Price of A.A unit of product B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
The objective function for this problem is?
A)
B)
C)
D)
)10 * Price of A.A unit of product B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
The objective function for this problem is?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What formula goes in cell B11 in this problem?
A)=B3*B7+B9/B3*B6+B9*2+B5*B7
B)=B3*B5+B3/B9*B6+B9/2*B5*B7
C)=SQRTB3*B5+B3/B9*B6+B9/2*B5*B7)
D)=B3*B3+B3/B9+B6*B9/2*B5*B7
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What formula goes in cell B11 in this problem?
A)=B3*B7+B9/B3*B6+B9*2+B5*B7
B)=B3*B5+B3/B9*B6+B9/2*B5*B7
C)=SQRTB3*B5+B3/B9*B6+B9/2*B5*B7)
D)=B3*B3+B3/B9+B6*B9/2*B5*B7

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
39
Why does the GRG algorithm not provide allowable increase or allowable decrease information with the Reduced Gradient and Lagrange multiplier information?
A)Because all constraints have slack.
B)Because the constraints may not be linear.
C)Because the solution is not necessarily a global optimum.
D)Because the solutions are not necessarily corner points.
A)Because all constraints have slack.
B)Because the constraints may not be linear.
C)Because the solution is not necessarily a global optimum.
D)Because the solutions are not necessarily corner points.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
40
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What constraint would you impose on this problem to ensure that at least one order is placed per year?
A)MAX B9
B)B9 = 1
C)B9 ? 1
D)MIN B11
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A.A unit of B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs

-An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses.Annual demand is 20,000 units and each cartridge costs the store $25.It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item.The following spreadsheet has been set up to solve the problem.What constraint would you impose on this problem to ensure that at least one order is placed per year?
A)MAX B9
B)B9 = 1
C)B9 ? 1
D)MIN B11

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
41
An investor is developing a portfolio of stocks.She has identified 3 stocks in which to invest.She wants to earn at least 11% return but with minimum risk.
Let: Pi = proportion of total funds invested in i,i = A,B,C The NLP for this problem is:

What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
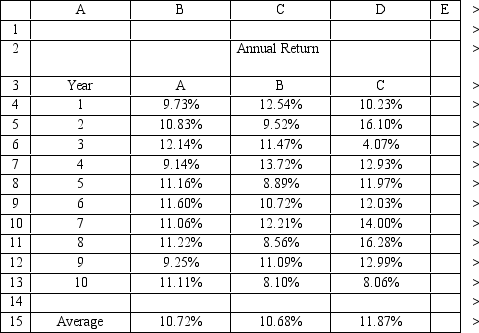
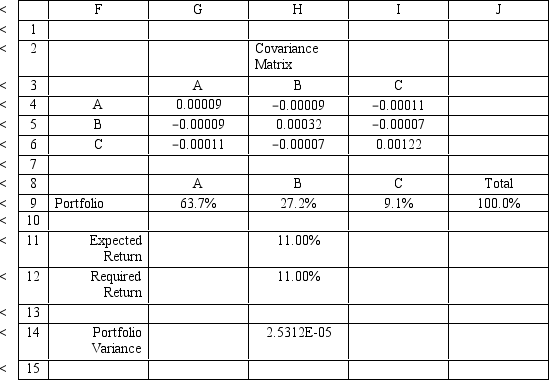
Let: Pi = proportion of total funds invested in i,i = A,B,C The NLP for this problem is:

What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.



Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
42
A company wants to locate a new warehouse to minimize the distance travelled by its delivery trucks.It has four stores and their coordinates are listed in the below.
Formulate the objective function for this problem.Let X and Y represent the X,Y coordinates of the new warehouse.
Formulate the objective function for this problem.Let X and Y represent the X,Y coordinates of the new warehouse.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
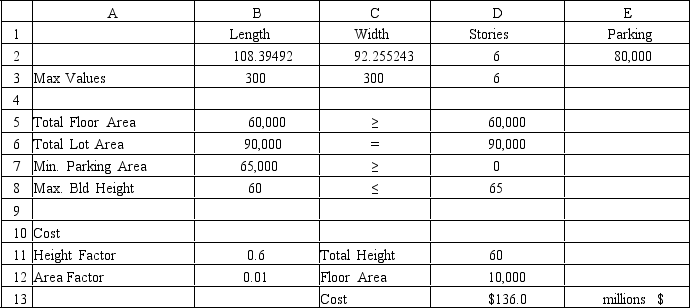
Refer to Exhibit 8.2.What formula would you place into cell B5 to calculate Total Floor Area?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
Refer to Exhibit 8.2.What formula would you place into cell B5 to calculate Total Floor Area?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
44
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
Formulate the NLP for the problem.
Formulate the NLP for the problem.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
45
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.

Refer to Exhibit 8.2.What formula would you place in cell D13 to calculate total cost?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
Refer to Exhibit 8.2.What formula would you place in cell D13 to calculate total cost?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
46
The main difference between linear LP)and nonlinear programming problems NLP)is that
A)NLP must have a nonlinear objective function
B)Some constraints in NLP may be nonlinear
C)No interaction terms are allowed in NLP
D)Only one constraint in NLP can be nonlinear
A)NLP must have a nonlinear objective function
B)Some constraints in NLP may be nonlinear
C)No interaction terms are allowed in NLP
D)Only one constraint in NLP can be nonlinear

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
47
A company wants to locate a new warehouse to minimize the longest distance travelled by any of its delivery trucks.It has four stores and their coordinates are listed in the below.
Formulate the NLP for this problem.Let X and Y represent the X,Y coordinates of the new warehouse.
Formulate the NLP for this problem.Let X and Y represent the X,Y coordinates of the new warehouse.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
48
An office supply company is attempting to determine the order quantity for Mt.White fountain pens which are sold to local executives.Annual demand is 5,000 units and each pen costs the store $50.It costs $75 to place an order and the inventory carrying cost rate is 30% of the value of the item.
What values should go in cells B3:B11 of the spreadsheet for this problem if Q = 223.61?
What values should go in cells B3:B11 of the spreadsheet for this problem if Q = 223.61?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
49
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 30 to make and demand is estimated to be 50 ? 0.09 * Price of A.A unit of B costs 20 to make and demand is estimated to be 30 ? 0.14 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 90 and 140.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
The NLP for the problem is:
What values should go in cells B3:E18 of the spreadsheet for this problem?
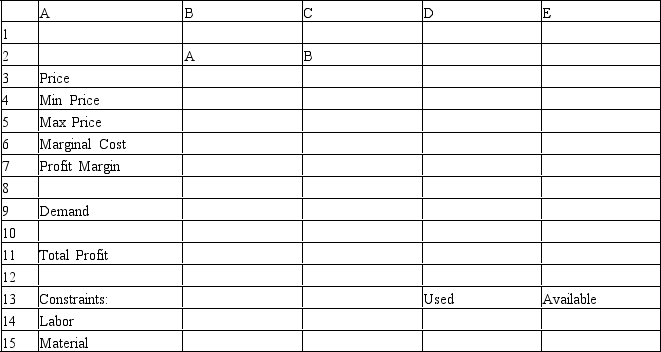
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
The NLP for the problem is:
What values should go in cells B3:E18 of the spreadsheet for this problem?


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
50
A company makes products A and B from 2 resources,labor and material.The company wants to determine the selling price which will maximize profits.A unit of A costs 30 to make and demand is estimated to be 50 ? .09 * Price of A.A unit of B costs 20 to make and demand is estimated to be 30 ? .14 * Price of B.The utilization of labor and materials and the available quantity of resources is shown in the table.A reasonable price for the products is between 90 and 140.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
Formulate the NLP for this company
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
Formulate the NLP for this company

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.

Refer to Exhibit 8.2.What formula would you place in cell B6 to calculate Total Lot Area?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
Refer to Exhibit 8.2.What formula would you place in cell B6 to calculate Total Lot Area?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
52
Calculate the annual inventory costs for the following data.
Order quantity = 400 units
Annual demand = 12,500 units
Unit purchase cost = 50
Fixed cost of placing an order = 75
Percentage cost of holding one unit in inventory for a year = 20%
Order quantity = 400 units
Annual demand = 12,500 units
Unit purchase cost = 50
Fixed cost of placing an order = 75
Percentage cost of holding one unit in inventory for a year = 20%

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
53
How many local minimum solutions are there on this graph of a function Mark their locations on the graph. 


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
54
The main difference between linear LP)and nonlinear programming problems NLP)is that
A)NLP may have a nonlinear objective function
B)All constraints in NLP must be nonlinear
C)No interaction terms are allowed in NLP
D)Only one constraint in NLP can be nonlinear
A)NLP may have a nonlinear objective function
B)All constraints in NLP must be nonlinear
C)No interaction terms are allowed in NLP
D)Only one constraint in NLP can be nonlinear

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
55
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments.The problem is summarized in the accompanying spreadsheet.The investor has enough money to make an initial investment of $12,000 and hopes he can earn 18% on his investments.He would like to know how low his annual return can be and still allow him to make his payments from interest income.
If the Analytic Solver Platform is used,which are the Objective,Variables and Constraint cells in the spreadsheet for this problem?
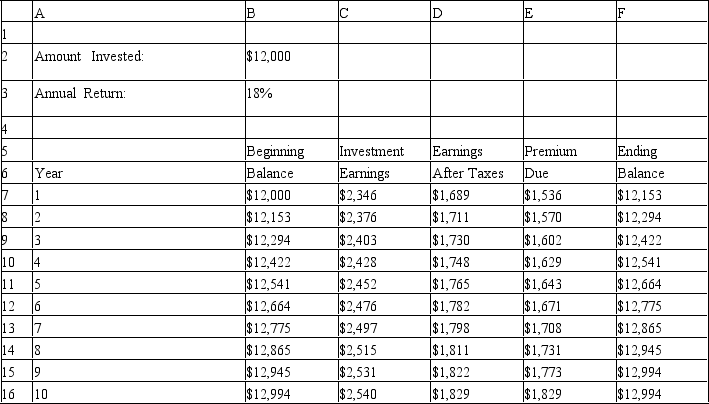
If the Analytic Solver Platform is used,which are the Objective,Variables and Constraint cells in the spreadsheet for this problem?


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
56
The Sweet Water beverage company is designing a new soft drink can.The designers wish to minimize the manufacturing cost of the can,a cost that is directly related to the amount of aluminum used in the can.The can must hold at least 350 ml or cm3)of beverage,have a diameter between 3 and 7 cm,and have a height between 7 and 19 cm.
Formulate the NLP for Sweet Water.
Formulate the NLP for Sweet Water.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
57
Find the maximum solution on this graph of a function starting from X = 12.Mark its location on the graph. 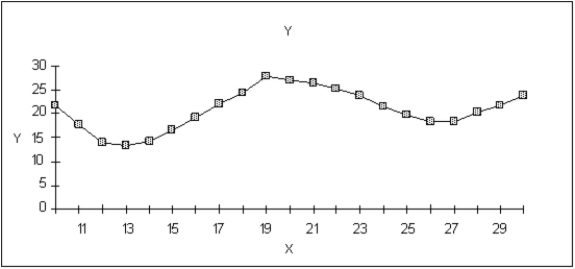


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
58
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.

-Refer to Exhibit 8.2.What values would you enter in the Analytic Solver Platform task pane for the above Excel spreadsheet?
Objective Cell: Variables Cells: Constraints Cells:
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2.What values would you enter in the Analytic Solver Platform task pane for the above Excel spreadsheet?
Objective Cell: Variables Cells: Constraints Cells:

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
59
An office supply company is attempting to determine the order quantity for Mt.White fountain pens which are sold to local executives.Annual demand is 5,000 units and each pen costs the store $50.It costs $75 to place an order and the inventory carrying cost rate is 30% of the value of the item.
Formulate the objective function for this problem.Let Q indicate the order quantity.
Formulate the objective function for this problem.Let Q indicate the order quantity.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
60
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.

Refer to Exhibit 8.2.The company wishes to have a relatively square building.Thus,they wish neither the building length nor the building width exceed the other by more than 25%.Add constraints)to enforce this design constraint.
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 × 300 foot lot upon which they plan to build an office building.They need at least 60,000 ft2 of office floor space.Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height.Further,parking space must equal at least 30% of the total floor space available.The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
Refer to Exhibit 8.2.The company wishes to have a relatively square building.Thus,they wish neither the building length nor the building width exceed the other by more than 25%.Add constraints)to enforce this design constraint.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
61
In solving the NLP problem,Solver produced a message "Solver has converged to the current solution.All constraints are satisfied." This means that:
A)Solver found a local optimal solution
B)Solver found a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)Your model is degenerate
A)Solver found a local optimal solution
B)Solver found a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)Your model is degenerate

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
62
The main difference between shadow prices and Lagrange multipliers is
A)the range of RHS values over which the Lagrange multipliers or the shadow prices remain valid
B)that shadow prices overestimate the impact of a small change in the RHS of the constraints on the objective function
C)that shadow prices underestimate the impact of a small change in the RHS of the constraints on the objective function
D)they are equivalent
A)the range of RHS values over which the Lagrange multipliers or the shadow prices remain valid
B)that shadow prices overestimate the impact of a small change in the RHS of the constraints on the objective function
C)that shadow prices underestimate the impact of a small change in the RHS of the constraints on the objective function
D)they are equivalent

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
63
The global optimum solution to a nonlinear programming problems NLP),in which the objective function must be maximized,is:
A)always larger than the local optimum solution
B)always smaller than the local optimum solution
C)is smaller or equal to the local optimum solution
D)is larger or equal to the local optimum solution
A)always larger than the local optimum solution
B)always smaller than the local optimum solution
C)is smaller or equal to the local optimum solution
D)is larger or equal to the local optimum solution

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
64
In solving the NLP problem,Solver produced a message "Solver found a solution.All constraints and optimality conditions are satisfied." This means that Solver found:
A)a local optimal solution
B)a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)a degenerate model
A)a local optimal solution
B)a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)a degenerate model

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
65
The global optimum solution to a nonlinear programming problems NLP),in which the objective function must be minimized,is:
A)always larger than the local optimum solution
B)always smaller than the local optimum solution
C)is smaller or equal to the local optimum solution
D)is larger or equal to the local optimum solution
A)always larger than the local optimum solution
B)always smaller than the local optimum solution
C)is smaller or equal to the local optimum solution
D)is larger or equal to the local optimum solution

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
66
In solving the NLP problem,Solver found a degenerate model.This means that:
A)Solver is cycling and redundant constraints must be removed
B)a global optimal solution was found
C)the objective function changed very slowly for the last few iterations
D)a local optimum was found
A)Solver is cycling and redundant constraints must be removed
B)a global optimal solution was found
C)the objective function changed very slowly for the last few iterations
D)a local optimum was found

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
67
In solving the NLP problem,Solver produced a message "Solver cannot improve the current solution.All constraints are satisfied." This means that Solver found:
A)a local optimal solution
B)a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)a degenerate model
A)a local optimal solution
B)a global optimal solution
C)the objective function changed very slowly for the last few iterations
D)a degenerate model

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
68
A nonzero reduced gradient value indicates the approximate impact
A)on the objective function of very small changes in the value of a given variable
B)on the RHS of a constraint of a unitary change in the objective function value
C)on the objective function of very large changes in the value of a given variable
D)on the objective function of unitary change in the RHS of associated constraint
A)on the objective function of very small changes in the value of a given variable
B)on the RHS of a constraint of a unitary change in the objective function value
C)on the objective function of very large changes in the value of a given variable
D)on the objective function of unitary change in the RHS of associated constraint

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
69
The Lagrange multipliers can be used to
A)estimate the impact of a small change in the RHS of the constraints on the objective function
B)estimate the impact of an arbitrary change in the RHS of the constraints on the objective function
C)estimate the impact of a small change in the RHS of the constraints on the shadow prices
D)estimate the impact of a large change in the RHS of the constraints on the shadow prices
A)estimate the impact of a small change in the RHS of the constraints on the objective function
B)estimate the impact of an arbitrary change in the RHS of the constraints on the objective function
C)estimate the impact of a small change in the RHS of the constraints on the shadow prices
D)estimate the impact of a large change in the RHS of the constraints on the shadow prices

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck



