Deck 7: The Trigonometric Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 7: The Trigonometric Functions
1
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the given angle:
A) , , is undefined, is undefined, , .
B) , , , , is undefined, is undefined.
C) , , is undefined, is undefined, , .
D) , , , , is undefined, is undefined.
E) , , is undefined, is undefined, , .
A) , , is undefined, is undefined, , .
B) , , , , is undefined, is undefined.
C) , , is undefined, is undefined, , .
D) , , , , is undefined, is undefined.
E) , , is undefined, is undefined, , .
, , is undefined, is undefined, , .
2
Rewrite in terms of sine and cosine, and simplify the expression:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Rewrite in terms of sine and cosine, and simplify the expression:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Use the definition to determine the radian measure of the angle. 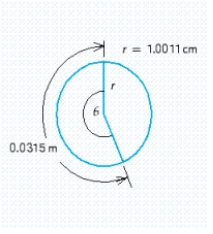
A) radians
B) radians
C) radians
D) radians
E) radians

A) radians
B) radians
C) radians
D) radians
E) radians

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Use the definition to determine the radian measure of the angle in the figure below. 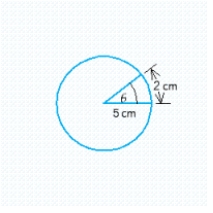
A) radians
B) radians
C) radians
D) radians
E) radians

A) radians
B) radians
C) radians
D) radians
E) radians

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the expressions using reference angles.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Let denote the point where the terminal side of angle (in standard position) meets the unit circle. Use the information to evaluate the six trigonometric functions of . is in Quadrant IV and .
A) , , , , ,
B) , , , , ,
C) , , , , ,
D) , ,
E) , , , , ,
A) , , , , ,
B) , , , , ,
C) , , , , ,
D) , ,
E) , , , , ,

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Refer to the figure, which shows all of the angles from to that are multiples of or . 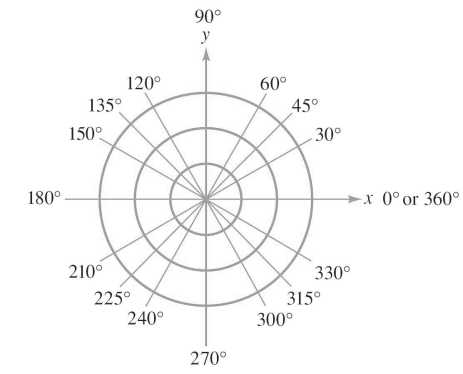 Relabel the angles in Quadrant III and IV using radian measure.
Relabel the angles in Quadrant III and IV using radian measure.
A)
B)
C)
D)
E)
 Relabel the angles in Quadrant III and IV using radian measure.
Relabel the angles in Quadrant III and IV using radian measure.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the given angle:
A) , , , , is undefined, is undefined.
B) , , is undefined, is undefined. , .
C) , , , , is undefined, is undefined.
D) , , is undefined, is undefined. , .
E) , , , , is undefined, is undefined.
A) , , , , is undefined, is undefined.
B) , , is undefined, is undefined. , .
C) , , , , is undefined, is undefined.
D) , , is undefined, is undefined. , .
E) , , , , is undefined, is undefined.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
You are given the rate of rotation of a wheel as well as its radius. Determine the following: (a) the angular speed, in units of radians/sec; (b) the linear speed, in units of cm/sec, of a point on the circumference of the wheel; (c) and the linear speed, in cm/sec, of a point halfway between the center of the wheel and the circumference. rpm; cm
A) (a) 156 radian/sec,
(b) 780 cm/sec,
(c) 390 cm/sec
B) (a)
(b) 1,278 cm/sec,
(c) 400 cm/sec
C) (a) radian/sec,
(b) 1,248 cm/sec,
(c) 624 cm/sec
D) (a) 520 radian/sec,
(b) 780 cm/sec,
(c) 1,560 cm/sec
E) (a) radian/sec,
(b) 780 cm/sec,
(c) 390 cm/sec
A) (a) 156 radian/sec,
(b) 780 cm/sec,
(c) 390 cm/sec
B) (a)
(b) 1,278 cm/sec,
(c) 400 cm/sec
C) (a) radian/sec,
(b) 1,248 cm/sec,
(c) 624 cm/sec
D) (a) 520 radian/sec,
(b) 780 cm/sec,
(c) 1,560 cm/sec
E) (a) radian/sec,
(b) 780 cm/sec,
(c) 390 cm/sec

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
Use a calculator to evaluate , , and for the value of . Round the answers to two decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Refer to the figure, which indicates radian measure on the unit circle for angles in standard position. Use the figure (and the unit circle definitions) to determine whether and are positive or negative. 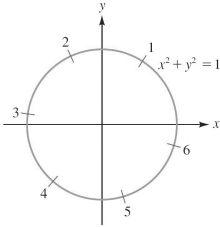
A) is positive, is positive, is negative
B) is negative, is positive, is negative
C) is positive, is positive, is positive
D) is positive, is negative, is positive
E) is negative, is negative, is positive

A) is positive, is positive, is negative
B) is negative, is positive, is negative
C) is positive, is positive, is positive
D) is positive, is negative, is positive
E) is negative, is negative, is positive

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
When a clock reads , what is the radian measure of the (smaller) angle between the hour hand and the minute hand?
A) radians
B) radians
C) radians
D) radians
E) radians
A) radians
B) radians
C) radians
D) radians
E) radians

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Use the figure to approximate the trigonometric values to within successive tenths. Then use a calculator to compute the values to the nearest hundredth. and 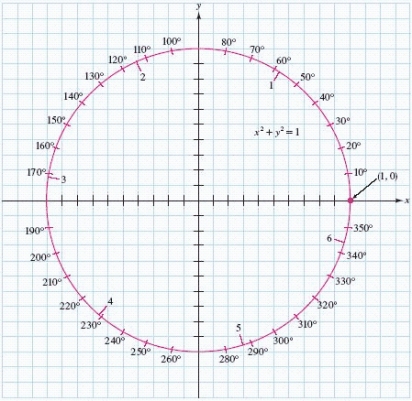
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Refer to the figure, which shows all of the angles from to that are multiples of or . 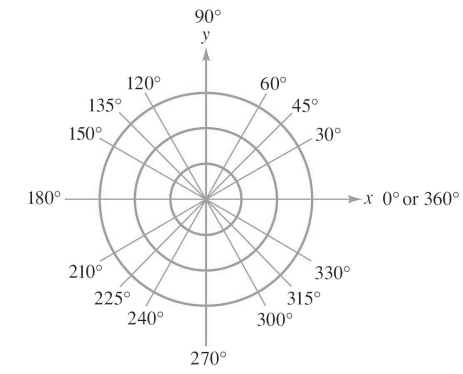 Relabel the angles in Quadrant I and II using radian measure.
Relabel the angles in Quadrant I and II using radian measure.
A)
B)
C)
D)
E)
 Relabel the angles in Quadrant I and II using radian measure.
Relabel the angles in Quadrant I and II using radian measure.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the expressions using reference angles.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the given angle:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Match an appropriate value from the right-hand column with each expression in the left-hand column.
a.
A.
b.
B.
c.
C.
d.
D.
E.
F.
A)
B)
C)
D)
E)
a.
A.
b.
B.
c.
C.
d.
D.
E.
F.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Simplify the expression and enter the answer in terms of sine and cosine.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose that is a right triangle with . If and , find the quantities. .
A) , , , , ,
B) , , , , ,
C) , , , , ,
D) , , , , ,
E) , , , , ,
A) , , , , ,
B) , , , , ,
C) , , , , ,
D) , , , , ,
E) , , , , ,

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Rewrite in terms of sine and cosine, and simplify the expression:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following is equal to:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following is equal to:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck



