Deck 6: Distribution and Network Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 6: Distribution and Network Models
1
The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.
True
2
The maximal flow problem can be formulated as a capacitated transshipment problem and determines the maximum amount of flow (such as messages,vehicles,fluid,etc.)that can enter and exit a network system in a given period of time.
True
3
If a transportation problem has four origins and five destinations,the LP formulation of the problem will have nine constraints.
True
4
When the number of agents exceeds the number of tasks in an assignment problem,one or more dummy tasks must be introduced in the LP formulation or else the LP will not have a feasible solution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
Transshipment problems allow shipments both in and out of some nodes,while transportation problems do not.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
A transportation problem with three sources and four destinations will have seven variables in the objective function.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
When a transportation problem has capacity limitations on one or more of its routes,it is known as a capacitated transportation problem.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
The shortest-route problem is a special case of the transshipment problem.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
The assignment problem is a special case of the transportation problem in which one agent is assigned to one,and only one,task.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
A transportation problem with three sources and four destinations will have seven decision variables.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11
A transshipment problem is a generalization of the transportation problem in which certain nodes are neither supply nodes nor destination nodes.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
In an assignment problem,one agent can be assigned to several tasks.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
Whenever total supply is less than total demand in a transportation problem,the LP model does not determine how the unsatisfied demand is handled.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
A transshipment constraint must contain a variable for every arc entering or leaving the node.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
When a route in a transportation problem is unacceptable,the corresponding variable can be removed from the LP formulation.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
Flow in a transportation network is limited to one direction.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
In a transportation problem with total supply equal to total demand,if there are four origins and seven destinations,and there is a unique optimal solution,the optimal solution will utilize 11 shipping routes.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
In the LP formulation of a maximal flow problem,a conservation of flow constraint ensures that an arc's flow capacity is not exceeded.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
A dummy origin in a transportation problem is used when supply exceeds demand.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
In a capacitated transshipment problem,some or all of the transfer points are subject to capacity restrictions.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
The problem that deals with the distribution of goods from several sources to several destinations is a(n)
A)maximal flow problem.
B)transportation problem.
C)assignment problem.
D)shortest-route problem.
A)maximal flow problem.
B)transportation problem.
C)assignment problem.
D)shortest-route problem.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following is NOT true regarding an LP model of the assignment problem?
A)Costs appear in the objective function only.
B)All constraints are of the ≥ form.
C)All constraint left-hand-side coefficient values are 1.
D)All decision variable values are either 0 or 1.
A)Costs appear in the objective function only.
B)All constraints are of the ≥ form.
C)All constraint left-hand-side coefficient values are 1.
D)All decision variable values are either 0 or 1.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
Consider a maximal flow problem in which vehicle traffic entering a city is routed among several routes before eventually leaving the city.When represented with a network,
A)the nodes represent stoplights.
B)the arcs represent one-way streets.
C)the nodes represent locations where speed limits change.
D)None of these are correct.
A)the nodes represent stoplights.
B)the arcs represent one-way streets.
C)the nodes represent locations where speed limits change.
D)None of these are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
There are two specific types of problems common in supply chain models that can be solved using linear programing: transportation problems and transshipment problems.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
The shortest-route problem finds the shortest route
A)from the source to any other node.
B)from any node to any other node.
C)from any node to the destination.
D)None of these are correct.
A)from the source to any other node.
B)from any node to any other node.
C)from any node to the destination.
D)None of these are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
The difference between the transportation and assignment problems is that
A)total supply must equal total demand in the transportation problem.
B)the number of origins must equal the number of destinations in the transportation problem.
C)each supply and demand value is 1 in the assignment problem.
D)there are many differences between the transportation and assignment problems.
A)total supply must equal total demand in the transportation problem.
B)the number of origins must equal the number of destinations in the transportation problem.
C)each supply and demand value is 1 in the assignment problem.
D)there are many differences between the transportation and assignment problems.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
Constraints in a transshipment problem
A)correspond to arcs.
B)include a variable for every arc.
C)require the sum of the shipments out of an origin node to equal supply.
D)All of these are correct.
A)correspond to arcs.
B)include a variable for every arc.
C)require the sum of the shipments out of an origin node to equal supply.
D)All of these are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
In a transportation problem,excess supply will appear as slack in the linear programming solution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
In a transshipment problem,shipments
A)cannot occur between two origin nodes.
B)cannot occur between an origin node and a destination node.
C)cannot occur between a transshipment node and a destination node.
D)can occur between any two nodes.
A)cannot occur between two origin nodes.
B)cannot occur between an origin node and a destination node.
C)cannot occur between a transshipment node and a destination node.
D)can occur between any two nodes.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following is NOT true regarding the linear programming formulation of a transportation problem?
A)Costs appear only in the objective function.
B)The number of variables is calculated as number of origins times number of destinations.
C)The number of constraints is calculated as number of origins times number of destinations.
D)The constraints' left-hand-side coefficients are either 0 or 1.
A)Costs appear only in the objective function.
B)The number of variables is calculated as number of origins times number of destinations.
C)The number of constraints is calculated as number of origins times number of destinations.
D)The constraints' left-hand-side coefficients are either 0 or 1.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
Consider a shortest-route problem in which a bank courier must travel between branches and the main operations center.When represented with a network,
A)the branches are the arcs and the operations center is the node.
B)the branches are the nodes and the operations center is the source.
C)the branches and the operations center are all nodes and the streets are the arcs.
D)the branches are the network and the operations center is the node.
A)the branches are the arcs and the operations center is the node.
B)the branches are the nodes and the operations center is the source.
C)the branches and the operations center are all nodes and the streets are the arcs.
D)the branches are the network and the operations center is the node.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
We represent the number of units shipped from origin i to destination j by
A)xij .
B)xji .
C)oij .
D)oji .
A)xij .
B)xji .
C)oij .
D)oji .

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
The assignment problem is a special case of the
A)transportation problem.
B)transshipment problem.
C)maximal flow problem.
D)shortest-route problem.
A)transportation problem.
B)transshipment problem.
C)maximal flow problem.
D)shortest-route problem.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35
The objective of the transportation problem is to
A)identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost.
B)minimize the number of origins used to satisfy total demand at the destinations.
C)minimize the number of shipments necessary to satisfy total demand at the destinations.
D)minimize the cost of shipping products from several origins to several destinations.
A)identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost.
B)minimize the number of origins used to satisfy total demand at the destinations.
C)minimize the number of shipments necessary to satisfy total demand at the destinations.
D)minimize the cost of shipping products from several origins to several destinations.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
The assignment problem constraint x31 + x32 + x33 + x34 ≤ 2 means
A)agent 3 can be assigned to two tasks.
B)agent 2 can be assigned to three tasks.
C)a mixture of agents 1,2,3,and 4 will be assigned to tasks.
D)there is no feasible solution.
A)agent 3 can be assigned to two tasks.
B)agent 2 can be assigned to three tasks.
C)a mixture of agents 1,2,3,and 4 will be assigned to tasks.
D)there is no feasible solution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
Arcs in a transshipment problem
A)must connect every node to a transshipment node.
B)represent the cost of shipments.
C)indicate the direction of the flow.
D)All of these are correct.
A)must connect every node to a transshipment node.
B)represent the cost of shipments.
C)indicate the direction of the flow.
D)All of these are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
In a maximal flow problem,
A)the flow out of a node is less than the flow into the node.
B)the objective is to determine the maximum amount of flow that can enter and exit a network system in a given period of time.
C)the number of arcs entering a node is equal to the number of arcs exiting the node.
D)None of these are correct.
A)the flow out of a node is less than the flow into the node.
B)the objective is to determine the maximum amount of flow that can enter and exit a network system in a given period of time.
C)the number of arcs entering a node is equal to the number of arcs exiting the node.
D)None of these are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
The parts of a network that represent the origins are called
A)capacities.
B)flows.
C)nodes.
D)arcs.
A)capacities.
B)flows.
C)nodes.
D)arcs.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
In the general linear programming model of the assignment problem,
A)one agent can do parts of several tasks.
B)one task can be done by several agents.
C)each agent is assigned to its own best task.
D)one agent is assigned to one and only one task.
A)one agent can do parts of several tasks.
B)one task can be done by several agents.
C)each agent is assigned to its own best task.
D)one agent is assigned to one and only one task.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the following shortest-route problem involving seven cities.The distances between the cities are given below.Draw the network model for this problem and formulate the LP for finding the shortest route from City 1 to City 7. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
After some special presentations,the employees of AV Center have to move projectors back to classrooms.The table below indicates the buildings where the projectors are now (the sources),where they need to go (the destinations),and a measure of the distance between sites. 




Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
Peaches are to be transported from three orchard regions to two canneries.Intermediate stops at a consolidation station are possible. 
Shipment costs are shown in the table below.Where no cost is given,shipments are not possible.Where costs are shown,shipments are possible in either direction.Draw the network model for this problem.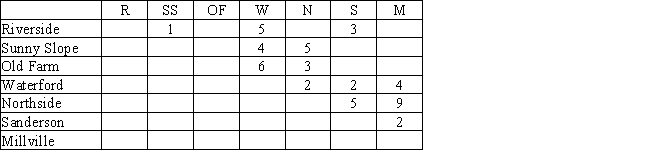

Shipment costs are shown in the table below.Where no cost is given,shipments are not possible.Where costs are shown,shipments are possible in either direction.Draw the network model for this problem.


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
The network below shows the flows possible between pairs of six locations.Formulate an LP to find the maximal flow possible from node 1 to node 6. 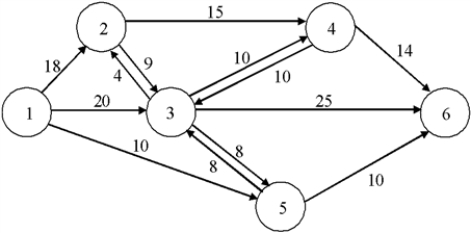


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
RVW (Restored Volkswagens)buys 15 used VW's at each of two car auctions each week held at different locations.It then transports the cars to repair shops it contracts with.When they are restored to RVW's specifications,RVW sells 10 each to three different used car lots.Various costs are associated with the average purchase and transportation prices from each auction to each repair shop.There are also transportation costs from the repair shops to the used car lots.RVW is concerned with minimizing its total cost given the costs in the table below. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
A foreman is trying to assign crews to produce the maximum number of parts per hour of a certain product.He has three crews and four possible work centers.The estimated number of parts per hour for each crew at each work center is summarized below.Solve for the optimal assignment of crews to work centers. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
Write the LP formulation for this transportation problem. 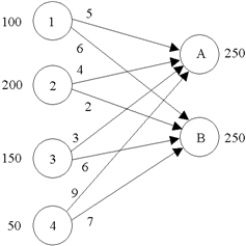


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
A network of railway lines connects the main lines entering and leaving a city.Speed limits,track reconstruction,and train length restrictions lead to the flow diagram below,where the numbers represent how many cars can pass per hour.Formulate an LP to find the maximal flow in cars per hour from node 1 to node F. 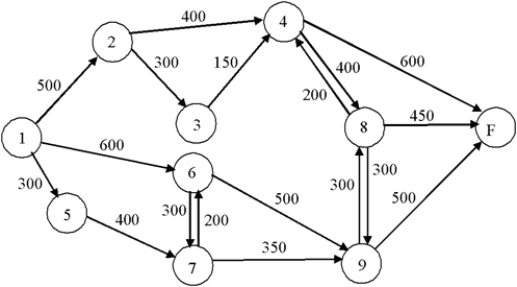


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the following shortest-route problem involving six cities with the distances given.Draw the network for this problem and formulate the LP for finding the shortest distance from City 1 to City 6. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
Show both the network and the linear programming formulation for this assignment problem. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51
Draw the network for this transportation problem. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
A professor has been contacted by four not-for-profit agencies that are willing to work with student consulting teams.The agencies need help with such things as budgeting,information systems,coordinating volunteers,and forecasting.Although each of the four student teams could work with any of the agencies,the professor feels that there is a difference in the amount of time it would take each group to solve each problem.The professor's estimate of the time,in days,is given in the table below.Use the computer solution to see which team works with which project. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
If a transportation problem has four origins and five destinations,the LP formulation of the problem will have
A)5 constraints.
B)9 constraints.
C)18 constraints.
D)20 constraints.
A)5 constraints.
B)9 constraints.
C)18 constraints.
D)20 constraints.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following is NOT a characteristic of assignment problems?
A)Costs appear in the objective function only.
B)The RHS of all constraints is 1.
C)The value of all decision variables is either 0 or 1.
D)The signs of constraints are always <.
A)Costs appear in the objective function only.
B)The RHS of all constraints is 1.
C)The value of all decision variables is either 0 or 1.
D)The signs of constraints are always <.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the network below.Formulate the LP for finding the shortest-route path from node 1 to node 7. 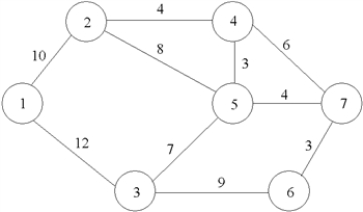


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
Write the linear program for this transshipment problem. 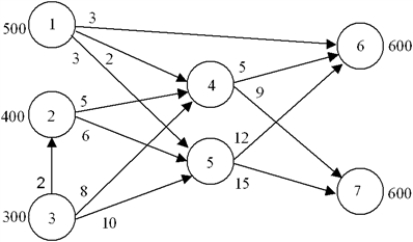


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
Canning Transport is to move goods from three factories to three distribution centers.Information about the move is given below.Give the network model and the linear programming model for this problem. 
Shipping costs are:

Shipping costs are:


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58
A beer distributor needs to plan how to make deliveries from its warehouse (node 1)to a supermarket (node 7),as shown in the network below.Develop the LP formulation for finding the shortest route from the warehouse to the supermarket. 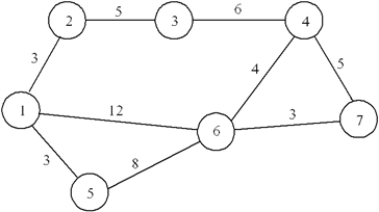


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
Draw the network for this assignment problem. 


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
The network flows into and out of demand nodes are what makes the production and inventory application modeled in the textbook a
A)shortest-route model.
B)maximal flow model.
C)transportation model.
D)transshipment model.
A)shortest-route model.
B)maximal flow model.
C)transportation model.
D)transshipment model.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
A plant manager for a sporting goods manufacturer is in charge of assigning the manufacture of four new aluminum products to four different departments.Because of varying expertise and workloads,the different departments can produce the new products at various rates.If only one product is to be produced by each department and the daily output rates are given in the table below,which department should manufacture which product to maximize total daily product output? (Note: Department 1 does not have the facilities to produce golf clubs.)
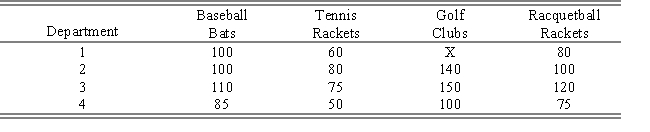
Formulate this assignment problem as a linear program.

Formulate this assignment problem as a linear program.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
A computer manufacturing company wants to develop a monthly plan for shipping finished products from three of its manufacturing facilities to three regional warehouses.It is thinking about using a transportation LP formulation to exactly match capacities and requirements.Data on transportation costs (in dollars per unit),capacities,and requirements are given below.
Warehouse
Plant 1 2 3 Capacities
A 2.41 1.63 2.09 4,000
B 3.18 5.62 1.74 6,000
C 4.12 3.16 3.09 3,000
Requirement 8,000 2,000 3,000
a.How many variables are involved in the LP formulation?
b.How many constraints are there in this problem?
c.What is the constraint corresponding to Plant B?
d.What is the constraint corresponding to Warehouse 3?
Warehouse
Plant 1 2 3 Capacities
A 2.41 1.63 2.09 4,000
B 3.18 5.62 1.74 6,000
C 4.12 3.16 3.09 3,000
Requirement 8,000 2,000 3,000
a.How many variables are involved in the LP formulation?
b.How many constraints are there in this problem?
c.What is the constraint corresponding to Plant B?
d.What is the constraint corresponding to Warehouse 3?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck



