Mel and Christy are co-workers with different risk attitudes. Both have investments in the stock market and hold U.S. Treasury securities (which provide the risk free rate of return). Mel's marginal rate of substitution of return for risk ( 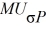
/ MU RP, σP) is

= 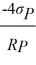
where RP is the individual's portfolio rate of return and σP is the individual's portfolio risk. Christy's 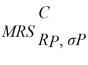
= 
. Each co-worker's budget constraint is RP = RF + 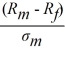
σP, where Rj is the risk-free rate of return, Rm is the stock market rate of return, and σm is the stock market risk. Solve for each co-worker's optimal portfolio rate of return as a function of Rj, Rm, and σm.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q125: The indifference curves of two investors are
Q141: Suppose an investor equally allocates their wealth
Q143: Is it possible for an investor to
Q146: Consider the following statements when answering this
Q148: Which of the following events will help
Q150: Which of the following statements is NOT
Q153: Which price index measures the change in
Q154: What is an informational cascade?
A) An excess
Q155: Donna is considering the option of becoming
Q157: What form of irrational behavior can cause
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents