The demand for action figures based on characters from children's movies is extremely high around the time the movie is released. In this peak period, demand for action figures is 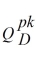
= 300,000 - 10,000P P = 30 - 0.0002 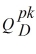
.
The resulting marginal revenue curve is MR(Qpk) = 30 - 0.0004 Qpk. Some time after the movie release, interest in the action figures wanes. In this lull period, demand for the action figures becomes 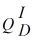
= 100,000 - 25,000P P = 4 - 0.00008 
. The resulting lull period marginal revenue curve is MR(QI) = 4 - 0.00016 QI. Suppose the marginal costs of producing the action figures are constant at $1.50. What is the optimal pricing strategy in the two different periods?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q91: Albatross Software has two main products: WindSong
Q92: Bookstores often offer annual memberships that allow
Q93: The Sneed Snack Shop sells hamburgers and
Q94: Internet service in the local market is
Q95: Internet service in the local market
Q97: There are two types of consumers
Q100: Marge's Beauty Salon sells shampoo and conditioner.
Q111: Cornucopia Media provides cable television service to
Q118: Which of the following statements is true?
A)
Q119: Hawkins MicroBrewery can influence demand by advertising.
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents