Use Stokes' Theorem to evaluate 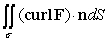 where F(x, y, z) = 11(z - y) i + 11(z2 + x) j + 11(x2 - y2) k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
where F(x, y, z) = 11(z - y) i + 11(z2 + x) j + 11(x2 - y2) k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
A) 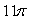
B) 
C) 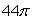
D) 
E) 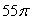
Correct Answer:
Verified
Q4: Use Stokes' Theorem to evaluate
Q5: Find the outward flux of the
Q6: Verify Stokes' Theorem if
Q7: Use Stokes' Theorem to evaluate
Q8: Use Stokes' Theorem to evaluate
Q10: Use Stokes' Theorem to evaluate
Q11: Use Stokes' Theorem to evaluate
Q12: Use Stokes' Theorem to evaluate
Q13: Use Stokes' Theorem to evaluate
Q14: Use Stokes' Theorem to evaluate 
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents