Multiple Choice
Use Stokes' Theorem to evaluate C 3(z - y) dx + 3(x - z) dy + 3(y - x) dz where C is the boundary, in the xy-plane, of the surface given by z = 4 - (x2 + y2) , z 0.
A) 
B) 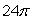
C) 0
D) 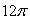
E) 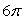
Correct Answer:
Verified
Related Questions
Q14: Use Stokes' Theorem to evaluate 
Q15: Use Stokes' Theorem to evaluate
Q16: Use Stokes' Theorem to evaluate
Q17: Use Stokes' Theorem to evaluate
Q18: Use Stokes' Theorem to evaluate 
Q20: Use Stokes' Theorem to evaluate
Q21: F (x, y, z) = 5xyz i
Q22: Use the divergence theorem to evaluate
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents