A company produces three products which must be painted, assembled, and inspected. The machinery must be cleaned and adjusted before each batch is produced. They want to maximize their profits for the amount of operating time they have. The unit profit and setup cost per batch are:
The operation time per unit and total operating hours available are:
Based on this ILP formulation of the problem and the optimal solution (X1, X2, X3) = (270, 0, 0), what values should appear in the shaded cells in the following Excel spreadsheet?
Xi = amount of product i produced
Yi = 1 if product i produced, 0 otherwise
MAX:
Subject to:
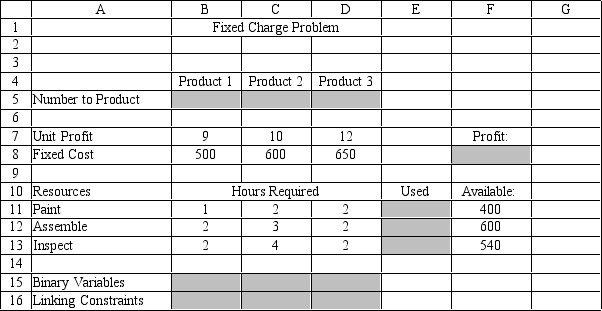
Correct Answer:
Verified
Q62: A company produces three products which
Q63: A cellular phone company wants to
Q64: The following ILP is being solved
Q68: A company needs to hire workers
Q69: A cellular phone company wants to
Q71: A certain military deployment requires supplies
Q72: A cellular phone company wants to
Q86: Exhibit 6.2
The following questions pertain to the
Q92: Exhibit 6.2
The following questions pertain to the
Q99: Exhibit 6.2
The following questions pertain to the
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents