TABLE 13-12
the Manager of the Purchasing Department of a Large

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { ations } & 30 \\\hline\end{array}\end{array}$$

$\begin{array}{lrrccc}\hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\\hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\\hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$





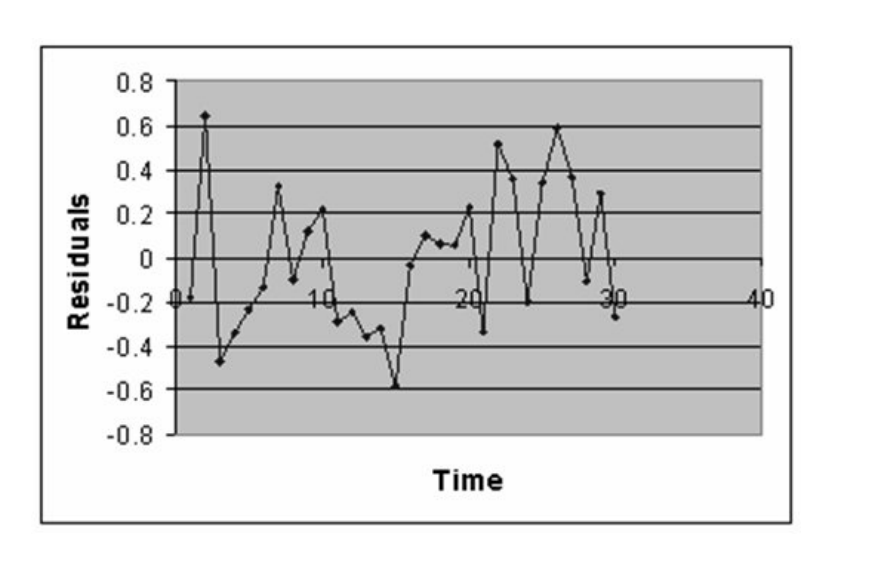
-Referring to Table 13-12, there is a 95% probability that the average amount of time needed to process one additional invoice is somewhere between 0.0109 and 0.0143 hours.