Solved

An Urn Contains 8 Red, 9 White, and 2 Black

Question 97

Multiple Choice

An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​


A) Pr(at least one B) = An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​ A) Pr(at least one B) = B) Pr(at least one B) = C) Pr(at least one B) = D) Pr(at least one B) = E) Pr(at least one B) =
B) Pr(at least one B) = An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​ A) Pr(at least one B) = B) Pr(at least one B) = C) Pr(at least one B) = D) Pr(at least one B) = E) Pr(at least one B) =
C) Pr(at least one B) = An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​ A) Pr(at least one B) = B) Pr(at least one B) = C) Pr(at least one B) = D) Pr(at least one B) = E) Pr(at least one B) =
D) Pr(at least one B) = An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​ A) Pr(at least one B) = B) Pr(at least one B) = C) Pr(at least one B) = D) Pr(at least one B) = E) Pr(at least one B) =
E) Pr(at least one B) = An urn contains 8 red, 9 white, and 2 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that at least one ball drawn is black B. ​ A) Pr(at least one B) = B) Pr(at least one B) = 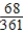C) Pr(at least one B) = 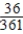D) Pr(at least one B) = 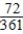E) Pr(at least one B) =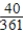

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q92: A bag contains 9 white balls W

Q93: Each of urns I and II has

Q94: A bag contains 7 white balls and

Q95: A bag contains 8 white balls and

Q96: A bag contains 5 coins, of which

Q98: Three balls are drawn, without replacement, from

Q99: Suppose a box contains 2 defective transistors

Q100: A bag contains 9 white balls and

Q101: Compute Compute .</p></div><svg width=

Q102: How many two-digit numbers can be formed

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents