Solved

The Following Sums of Squares Are Produced: 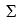(Yi-(Y-Bar))2 = 250

Question 9

Multiple Choice

The following sums of squares are produced: The following sums of squares are produced: (y<sub>i</sub>-(y-bar) ) <sup>2</sup> = 250, (y<sub>i</sub>-(y<sub>i</sub>-hat) ) <sup>2</sup> = 100, ((y<sub>i</sub>-hat) -(y-bar) ) <sup>2</sup> = 150 The percentage of the variation in y that is explained by the variation in x is: A) 60% . B) 75% . C) 40% . D) 50% .(yi-(y-bar) ) 2 = 250, 11ef1ab2_4bf1_c05d_a741_c73dacf30ae9_TB5762_11(yi-(yi-hat) ) 2 = 100, 11ef1ab2_4bf1_c05d_a741_c73dacf30ae9_TB5762_11((yi-hat) -(y-bar) ) 2 = 150
The percentage of the variation in y that is explained by the variation in x is:


A) 60% .
B) 75% .
C) 40% .
D) 50% .

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: The Spearman rank correlation coefficient must be

Q2: Given that the sum of squares for

Q4: Given that ssx = 2500, ssy =

Q6: Which value of the coefficient of correlation

Q7: In a simple linear regression, which of

Q8: If an estimated regression line has a

Q13: A regression line using 25 observations produced

Q13: The symbol for the population coefficient

Q17: If the coefficient of correlation is 0.80,

Q135: If all the points in a scatter

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents