Suppose that the actual proportion of people at a particular company who use their bicycles to travel to job is 0.35. In a study of bicycle parking places needs, administration would like to estimate this proportion. They plan to take a random sample of 50 employees and use the sample proportion who use bicycles, 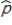 , as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is
, as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is 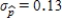 . Would you expect more or less sample-to-sample variability in the sample proportions than for when
. Would you expect more or less sample-to-sample variability in the sample proportions than for when 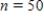 ? Is the sample size that resulted in
? Is the sample size that resulted in 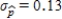 larger or smaller than 50?
larger or smaller than 50?
A) The standard deviation for the initial sample of the size  is
is  .Since the standard deviation
.Since the standard deviation 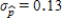 is greater than
is greater than 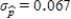 , sample-to-sample variability is less and the new sample size is smaller.
, sample-to-sample variability is less and the new sample size is smaller.
B) The standard deviation for the initial sample of the size 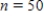 is
is 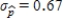 .Since the standard deviation
.Since the standard deviation 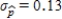 is less than
is less than 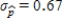 , sample-to-sample variability is more and the new sample size is larger.
, sample-to-sample variability is more and the new sample size is larger.
C) The standard deviation for the initial sample of the size  is
is 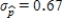 .Since the standard deviation
.Since the standard deviation 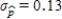 is greater than
is greater than 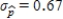 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.
D) The standard deviation for the initial sample of the size 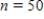 is
is 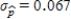 .Since the standard deviation
.Since the standard deviation 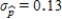 is greater than
is greater than 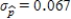 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.
E) The standard deviation for the initial sample of the size 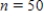 is
is 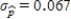 .Since the standard deviation
.Since the standard deviation  is greater than
is greater than 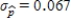 , sample-to-sample variability is less and the new sample size is larger.
, sample-to-sample variability is less and the new sample size is larger.
Correct Answer:
Verified
Q25: The first large-scale study of the human
Q26: Consider sampling from a population whose proportion
Q28: One method for estimating the availability of
Q29: Consider the following "population": {1, 1, 3,
Q30: Consider sampling from a skewed population. As
Q31: One method for estimating abundance of animals
Q32: Some biologists believe the evolution of handedness
Q34: How are the quantities, p and
Q35: The principal at Thomas Jefferson High School
Q37: When the sample size is "large enough,"
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents