A deck of 52 cards is mixed well, and 5 cards are dealt. It can be shown that (disregarding the order in which the cards are dealt) there are 2,598,960 possible hands, of which only 4 hands are royal flushes. (A royal flush is a hand consisting of 10, J, Q, K, and A, all of the same suit) .
What is the probability that a hand will be a royal flush?
A) 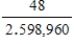
B) 
C) 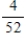
D) 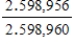
E) 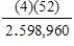
Correct Answer:
Verified
Q1: Two events are said to be disjoint
Q3: A chance experiment is any activity or
Q12: An airline reports that for a particular
Q13: Suppose you want to estimate the probability
Q14: A large cable company reports that 70%
Q16: A rental car company offers two options
Q18: The faces of a twelve-sided die are
Q20: The probability of an event E can
Q21: Investigators recently reported the results a study
Q21: The football team at North Snowshoe High
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents