Consider the following two games:
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)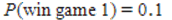 and
and  , therefore it is advantageous to play game 1 because the probability of winning is higher.
, therefore it is advantageous to play game 1 because the probability of winning is higher.
B)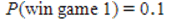 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
C)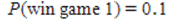 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
D)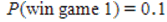 and
and 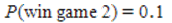 , therefore it is no matter what game to play because the probabilities of winning are equal.
, therefore it is no matter what game to play because the probabilities of winning are equal.
E)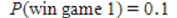 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
Correct Answer:
Verified
Q39: Consider the chance experiment in which a
Q40: In a few sentences, define the following
Q41: At Thomas Jefferson High School students are
Q42: A man has five ties and each
Q43: In a special report, "Speed Demons," in
Q45: In a particular city, 45% of donors
Q46: Experimental studies utilize blinding to prevent researchers
Q47: Three of the most common pets that
Q48: Exhibit 5-1
In a survey of airline travelers,
Q49: Suppose a survey was conducted among women
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents