Solved

When Issuing a Textbook, There Is Always a Number of Defective

Question 2

Multiple Choice

When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level.


A) When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats.
B) When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats.
C) When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. 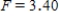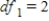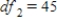, When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats.
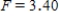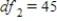D) When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. 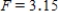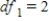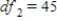, When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. 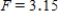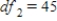, When issuing a textbook, there is always a number of defective copies. The publishing house conducts a study to determine whether the number of defective copies depends on the format of the textbook. For the study, three random samples of textbook editions for the different book sizes were generated: a large portrait, a portrait, and a US letter, each of is the editions has approximately equal number of copies. The number of defective copies for each edition is indicated in the table below. ​ Carry out an ANOVA F test and interpret the results using the 95% confidence level. A) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. B) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. C) , , , and p-value is less than 0.05.We reject the null hypothesis and can conclude that the average number of defective copies is not the same for the different textbook formats. D) , , , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats. , and p-value is greater than 0.05.We don't reject the null hypothesis and can conclude that the average number of defective copies is the same for the different textbook formats.

Correct Answer:

verifed

Verified

Related Questions

Q1: A course work of a student is

Q3: A researcher wants to know if people

Q4: The two main human blood group systems

Q5: A researcher wants to know if people

Q6: At a large construction website, a construction

Q7: A recruitment agency provides a study of

Q8: The two main human blood group systems

Q9: A graduate student of the college conducted

Q10: A researcher wants to find out if

Q11: Before releasing a new product, a small

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents