Researchers studied how many steps a day adult residents of the city make. They determined that the mean number of steps per day for a representative sample of 10 adult residents of the city was 5,139 steps. The original sample data values are:  Researchers are interested in deciding if there is evidence that adult residents of the city make more than 5,000 steps per day. Use a randomization test to select the appropriate output for one set of 1,000 simulated sample means and carry out a hypothesis test for a population mean.
Researchers are interested in deciding if there is evidence that adult residents of the city make more than 5,000 steps per day. Use a randomization test to select the appropriate output for one set of 1,000 simulated sample means and carry out a hypothesis test for a population mean.
A) 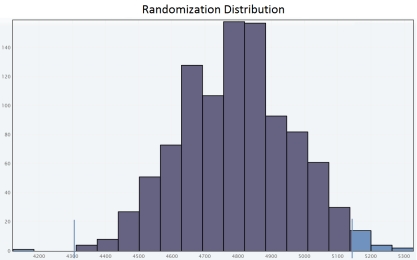
 Since the approximate P-value is less than
Since the approximate P-value is less than  , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
B) 
 Since the approximate P-value is greater than
Since the approximate P-value is greater than  , we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
C) 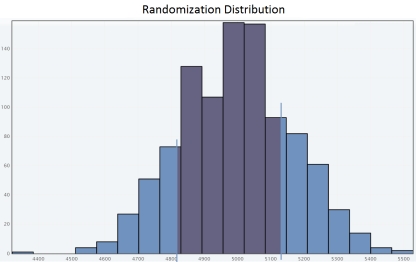

Since the approximate P-value is greater than  , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
D) 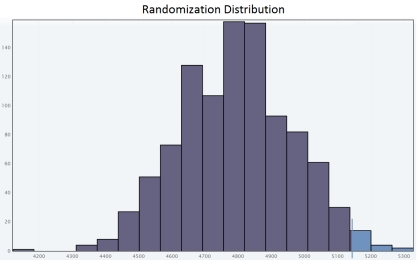

Since the approximate P-value is less than 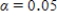 , we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
E) 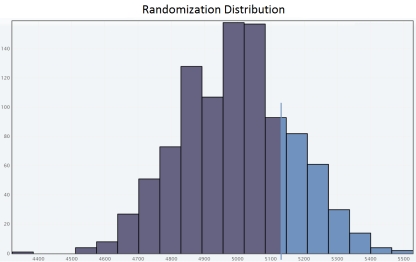

Since the approximate P-value is greater than 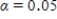 , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
Correct Answer:
Verified
Q8: In your own words, distinguish between "statistical"
Q16: Suppose that a study has been published
Q36: A company provides portable walkie-talkies to construction
Q42: Researchers studied the average height of 12
Q44: The lecturer decided to estimate the mean
Q45: Researchers studied how many emails a day
Q46: In an analysis of hunting by African
Q48: An important part of any dispensing process
Q50: Researchers conducted a survey among 1793 families
Q51: In an analysis of hunting by African
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents