Consider the population described by the probability distribution below. a. Find .
b. Find the sampling distribution of the sample mean for a random sample of measurements from this distribution.
c. Find the sampling distribution of the sample median for a random sample of observations from this population.
d. Show that both the mean and the median are unbiased estimators of for this population.
e. Find the variances of the sampling distributions of the sample mean and the sample median.
f. Which estimator would you use to estimate ? Why? 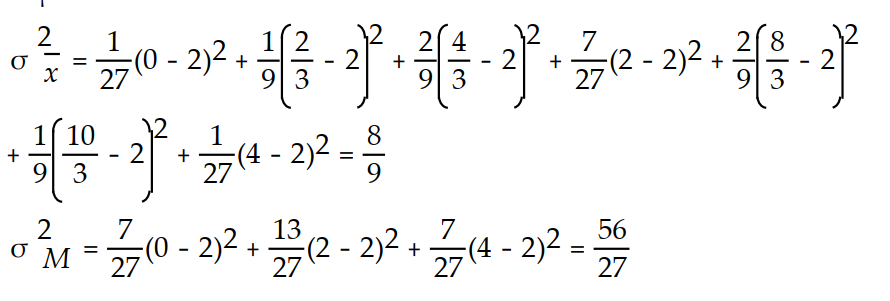
Correct Answer:
Verified
f. sa...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q4: Consider the population described by the
Q5: The amount of time it takes
Q6: The probability distribution shown below describes
Q7: A random sample of size n
Q8: Consider the probability distribution shown here.
Q10: Suppose a random sample of
Q12: Which of the following describes what the
Q13: Consider the population described by the
Q14: The probability distribution shown below describes
Q42: The weight of corn chips dispensed into
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents