Solve the problem.
-The strength S of a wooden beam with rectangular cross section is given by the formula where d is the diagonal length, the angle illustrated, and k is a constant that varies with the type of wood used. 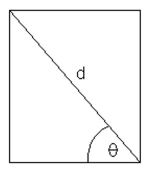 Let and express the strength in terms of the constant for , and . Does the strength always increase as gets larger?
Let and express the strength in terms of the constant for , and . Does the strength always increase as gets larger?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q137: Find the exact value of the
Q138: Find the exact value of the
Q139: Find the exact value of the
Q140: Find the exact value. Do not
Q141: Use a calculator to find the
Q143: Use a calculator to find the
Q144: Use a calculator to find the
Q145: Use a calculator to find the
Q146: A point on the terminal side
Q147: Use a calculator to find the
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents