Solve
-If the Three Lengths of the Sides of a Triangle

Solve.
-If the three lengths of the sides of a triangle are known, Heron's formula can be used to find its area. and $c$ are the three lengths of the sides, Heron's formula for area is:
$$A = \sqrt { s ( s - a ) ( s - b ) ( s - c ) }$$
where $s$ is half the perimeter of the triangle, or $s = \frac { 1 } { 2 } ( a + b + c )$ .
Use this formula to approximate the area of the triangle to two decimal places, if necessary, when a 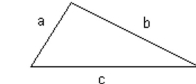$\mathrm { cm } , \mathrm { b } = 11 \mathrm {~cm}$ and $\mathrm { c } = 16 \mathrm {~cm}$ .

A) $47.62 \mathrm { sq } \mathrm { cm }$
B) $697.14 \mathrm { sq } \mathrm { cm }$
C) $9.76 \mathrm { sq } \mathrm { cm }$
D) $11.22 \mathrm { sq } \mathrm { cm }$ , b,