The Regression Below Predicts the Daily Number of Skiers Who $F$

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
R squared $= 25.4 \% \quad \mathrm { R }$ squared (adjusted) $= 16.8 \%$
$s = 125.1$ with $30 - 4 = 26$ degrees of freedom



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$



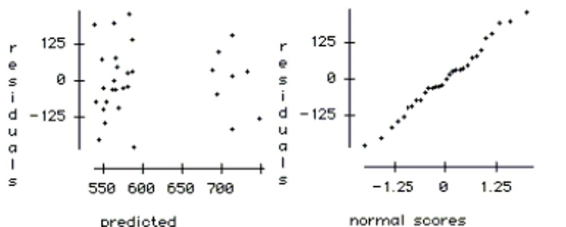
-If you think that the temperature might affect attendance differently on weekends than on
weekdays, how would you change the regression to test this?