Descent, Inc., produces a variety of climbing and mountaineering equipment. One of its products is a traditional three-strand climbing rope. An important characteristic of any climbing rope is its tensile strength. Descent produces the three-strand rope on two separate production lines: one in Bozeman and the other in Challis. The Bozeman line has recently installed new production equipment. Descent regularly tests the tensile strength of its ropes by randomly selecting ropes from production and subjecting them to various tests. The most recent random sample of ropes, taken after the new equipment was installed at the Bozeman plant, revealed the following: 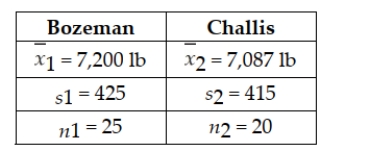 Descent's production managers are willing to assume that the population of tensile strengths for each plant is approximately normally distributed with equal variances. Based on the sample results, can Descent's managers conclude that there is a difference between the mean tensile strengths of ropes produced in Bozeman and Challis? Conduct the appropriate hypothesis test at the 0.05 level of significance.
Descent's production managers are willing to assume that the population of tensile strengths for each plant is approximately normally distributed with equal variances. Based on the sample results, can Descent's managers conclude that there is a difference between the mean tensile strengths of ropes produced in Bozeman and Challis? Conduct the appropriate hypothesis test at the 0.05 level of significance.
A) Because the calculated value of t = 0.896 is neither less than the lower tail critical value of t = -2.0167, nor greater than the upper tail critical value of t = 2.0167, do not reject the null hypothesis. Based on these
Sample data, at the α = 0.05 level of significance there is not sufficient evidence to conclude that the
Average tensile strength of ropes produced at the two plants is different.
B) Because the calculated value of t = 0.451 is neither less than the lower tail critical value of t = -2.0167, nor greater than the upper tail critical value of t = 2.0167, do not reject the null hypothesis. Based on these
Sample data, at the α = 0.05 level of significance there is not sufficient evidence to conclude that the
Average tensile strength of ropes produced at the two plants is different.
C) Because the calculated value of t = -2.8126 is less than the lower tail critical value of t = -2.0167, reject the null hypothesis. Based on these sample data, at the α = 0.05 level of significance there is sufficient
Evidence to conclude that the average tensile strength of ropes produced at the two plants is different.
D) Because the calculated value of t = 2.8126 is greater than the lower tail critical value of t = -2.0167, reject the null hypothesis. Based on these sample data, at the α = 0.05 level of significance there is sufficient
Evidence to conclude that the average tensile strength of ropes produced at the two plants is different.
Correct Answer:
Verified
Q104: A real estate agent believes that home
Q105: A major U.S. oil company has developed
Q106: In an article entitled "Childhood Pastimes Are
Q107: A PC company uses two suppliers for
Q108: Suppose as part of a national study
Q110: You are given the following results of
Q111: The management of the Seaside Golf Club
Q112: A major U.S. oil company has developed
Q113: The following samples are observations taken from
Q114: A paired sample study has been conducted
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents