Consider the poset with the following Hasse diagram. 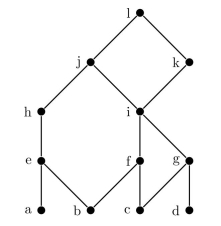
(a) Find all maximal elements of the poset.
(b) Find all minimal elements of the poset.
(c) Find the least element of the poset if it exists, or show that it does not exist.
(d) Find the greatest element of the poset if it exists, or show that it does not exist.
(e) What is the greatest lower bound of the set {a, b, c}?
(f) What is the least upper bound of the set {a, b, c}?
Correct Answer:
Verified
Q1: Show that the inclusion relation,
Q2: Show that the relation
Q4: What is the transitive closure of the
Q5: Which ordered pairs are in the relation
Q6: Suppose that R1 and R2 are symmetric
Q7: Find the reflexive closure and the symmetric
Q8: (a) Show that the relation
Q9: What is the join of the 3-ary
Q10: (a) Are the sets {1,3,6},{2,4,7} ,
Q11: What are the minimal and maximal elements
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents