Solve the Problem $1994 .$ Then Estimate the Country's Population, in Millions, in 2004

Solve the problem.
-The following table shows a country's population from 1995 to 1998: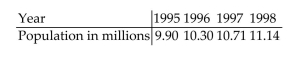

Divide the population for each year by the population in the preceding year. Use this ratio to write the general term of the geometric sequence describing the country's population growth n years after $1994 .$ Then estimate the country's population, in millions, in 2004 .

A) $\mathrm { a } _ { \mathrm { n } } = 9.90 ( 1.04 ) ^ { \mathrm { n } - 1 } ; 14.09$ million
B) $\mathrm { a } _ { \mathrm { n } } = 9.90 ( 1.04 ) ^ { \mathrm { n } - 1 } ; 14.65$ million
C) $\mathrm { a } _ { \mathrm { n } } = 9.90 ( 1.03 ) ^ { \mathrm { n } - 1 } ; 16.73$ million
D) $a _ { n } = 9.90 ( 1.03 ) ^ { n - 1 } ; 15.78$ million