Unicellular Yeasts Can Be Represented as Spheres, Whereas Filamentous Hyphae

Unicellular yeasts can be represented as spheres, whereas filamentous hyphae more closely resemble cylinders. As these two geometric figures increase in size, their surface area-to-volume ratios change. The following tables demonstrate how this ratio changes, first for spheres, and second for cylinders. For the cylinder, girth (i.e., radius, r) will remain constant, whereas length, L, will increase. Note the formulas below the respective tables.
A sphere's change in surface area and volume with increasing radius, r

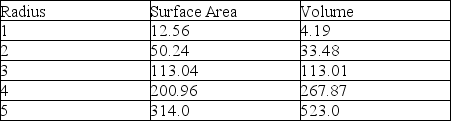
Area of a Sphere = 4r² Volume of a Sphere = 4/3r³
A cylinder's change in surface area and volume with increasing length, L

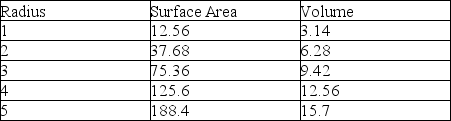
Area of a Cylinder = 2(r²) + 2rL Volume of a Cylinder = r²ᴸ
-As a direct result of increasing surface area in both yeasts and filamentous hyphae, which cell structures/materials must also increase?
1) amount of chitin
2) number of nuclei
3) amount of plasma membrane
4) number of mitochondria
5) amount of peptidoglycan

A) 1 only
B) 1 and 3
C) 2 and 3
D) 2 and 4
E) 1, 3, and 5