The wave function for a particle confined to a one-dimensional box located between x = 0 and x = L is given by Ψ(x) = A sin (nπx/L) + B cos (nπx/L) . The constants A and B are determined to be
A) 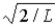 , 0
, 0
B) 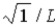 ,
,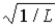
C) 0,
D) 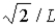 ,
,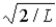
E) 2/L, 0
Correct Answer:
Verified
Q11: If the interaction of a particle with
Q12: Classically, the concept of "tunneling" is impossible.
Q13: A physically reasonable wave function, ψ(x), for
Q14: Find the kinetic energy (in terms of
Q15: What is the quantum number n of
Q17: What is the quantum number n of
Q18: Calculate the ground state energy (in eV)
Q19: The expectations value of a function f(x)
Q20: The wave function for a particle in
Q21: The wave function for a particle in
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents