Two independent samples sizes 20 and 30 are randomly selected from two normally distributed populations. Assume that the population variances are unknown but equal. To test the difference between the population means, 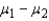 , the sampling distribution of the sample mean difference,
, the sampling distribution of the sample mean difference, 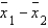 , is:
, is:
A) normally distributed
B) t-distributed with 50 degrees of freedom
C) t-distributed with 48 degrees of freedom
D) F-distributed with 19 and 29 degrees of freedom
E) z-distributed with 30 degrees of freedom
Correct Answer:
Verified
Q155: In testing the difference between two population
Q156: Two independent samples of sizes 40 and
Q157: The t-test for the difference between the
Q158: In testing whether the means of two
Q159: Two independent samples of sizes 25 and
Q161: The mean playing times (in hours) for
Q162: Two independent random samples of sizes
Q163: A child psychologist was interested in the
Q164: Assume that the population distributions of times
Q165: Thirty-five employees who completed two years of
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents