Assume that two independent random samples of sizes 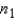 and
and 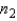 have been selected from binomial populations with parameters
have been selected from binomial populations with parameters 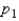 and
and 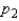 , respectively. The standard error of the sampling distribution of
, respectively. The standard error of the sampling distribution of 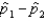 , the difference between sample proportions, is estimated by
, the difference between sample proportions, is estimated by  .
.
Correct Answer:
Verified
Q16: A 99% upper confidence bound (UCB) for
Q17: A 95% lower confidence bound (LCB) for
Q18: If you wish to construct 98% upper
Q19: Trish attends an aerobics class four times
Q20: The sample size needed to estimate a
Q22: Assume that two independent random samples of
Q23: A questionnaire is designed to investigate attitudes
Q24: If we wish to construct a 95%
Q25: If a 90% confidence interval estimate for
Q26: A process control engineer wishes to estimate
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents