Find the eccentricity and distance from the pole to the directrix of the conic. Then sketch and identify the graph. Use a graphing utility to confirm your results. 
A) eccentricity: 
Distance from pole to directrix: 
The graph is an ellipse.

B) eccentricity: 
Distance from pole to directrix: 
The graph is a hyperbola.

C) eccentricity: 
Distance from pole to directrix: 
The graph is a hyperbola.
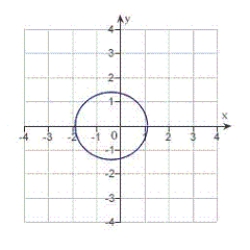
D) eccentricity: 
Distance from pole to directrix: 
The graph is an ellipse.
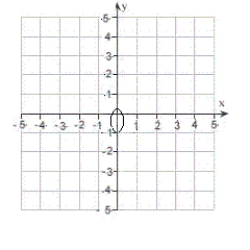
E) eccentricity: 
Distance from pole to directrix: 
The graph is an ellipse.
Correct Answer:
Verified
Q1: Find the corresponding rectangular coordinates for the
Q2: Match the graph with its polar equation.
Q3: Find the second derivative Q5: Find all points (if any) of horizontal Q6: Find the eccentricity of the ellipse given Q7: Match the equation with its graph. Q8: For the given point in rectangular coordinates, Q9: Identify the graph for the polar equation Q10: Find the area of the surface generated Q11: Match the graph with its polar equation.![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents