Multiple Choice
light on top of the car turns at a rate of revolution per second. The rate at which the light beam moves along the wall is . Find the limit of as .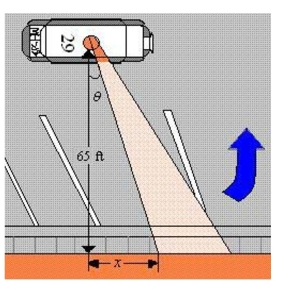
A)
B)
C) 0
D) 65
E)
Correct Answer:
Verified
Related Questions
Q82: Q83: Q84: Find the limit. Q85: Q86: Find the limit. Q88: Find the limit. Q89: 25-foot ladder is leaning against a Q90: Find the following limit if it Q91: A 30 -foot ladder is leaning Q92: Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents

