Multiple Choice
A petrol car is parked 40 feet from a long warehouse (see figure) . The revolving light on top 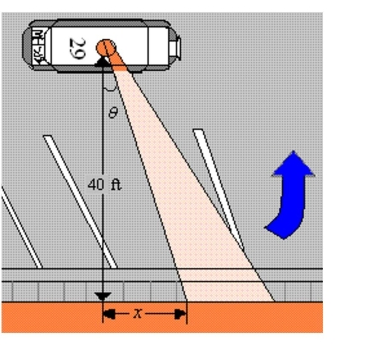
A)
B)
C)
D)
E)
Correct Answer:
Verified
Related Questions
Q160: Q161: A spherical balloon is inflated with Q162: Assume that x and y are Q163: Find the rate of change of Q164: Q166: ladder feet long is leaning against Q167: The radius r of a sphere Q168: A ladder feet long is leaning Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents

