Find the Particular Solution of the Differential Equation $\frac { w } { g } y ^ { tt } ( t ) + b y ^ { t } ( t ) + k y ( t ) = \frac { w } { g } F ( t )$

Find the particular solution of the differential equation $\frac { w } { g } y ^ { tt } ( t ) + b y ^ { t } ( t ) + k y ( t ) = \frac { w } { g } F ( t )$ for the oscillating motion of an object on the end of a spring. In the equation, $y$ is the displacement from equilibrium (positive direction is downward) measured in feet, and $t$ is the time in seconds (see figure) . The constant $w = 8$ is the weight of the object, $g = 128$ is the acceleration due to gravity, $b = 1$ is the magnitude of the resistance to the motion, $k = 4$ is the spring constant from Hooke's Law, $F ( t ) = 4 \sin 8 t$ is the acceleration imposed on the system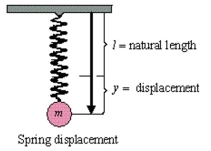, $y ( 0 ) = \frac { 1 } { 7 }$ and $y ^ {t } ( 0 ) = - 9$

A) $y = \left( \frac { 39 } { 224 } + \frac { 213 } { 28 } t \right) e ^ { - 8 t } - \frac { 1 } { 36 } \cos 8 t$
B) $y = \left( \frac { 39 } { 224 } - \frac { 213 } { 28 } t \right) e ^ { - 8 t } - \frac { 1 } { 32 } \cos 8 t$
C) $y = \left( \frac { 43 } { 252 } - \frac { 272 } { 35 } t \right) e ^ { - 8 t } - \frac { 1 } { 34 } \cos 8 t$
D) $y = \left( \frac { 43 } { 252 } + \frac { 272 } { 35 } t \right) e ^ { - 8 t } - \frac { 1 } { 30 } \cos 8 t$
E) $y = \left( \frac { 39 } { 224 } - \frac { 272 } { 35 } t \right) e ^ { - 8 t } - \frac { 1 } { 40 } \cos 8 t$