SCENARIO 18-6 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) .Two variables thought to affect weight-loss are client's length of time on the weight loss program and time of session.These variables are described below: Y = Weight-loss (in pounds) 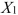 = Length of time in weight-loss program (in months)
= Length of time in weight-loss program (in months) 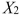 = 1 if morning session, 0 if not
= 1 if morning session, 0 if not 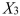 = 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
= 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: 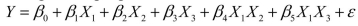 Partial output from Microsoft Excel follows:
Partial output from Microsoft Excel follows: 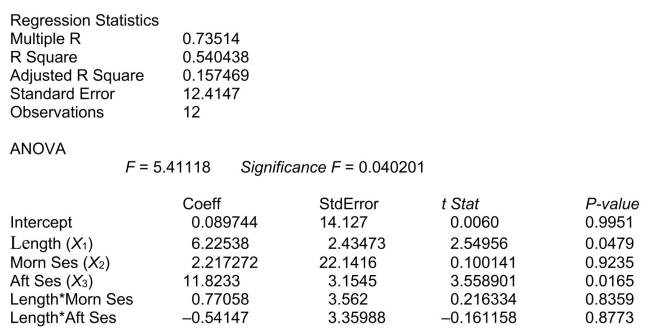
-Referring to Scenario 18-6, what null hypothesis would you test to determine whether the slope of the linear relationship between weight-loss (Y) and time in the program (x₁) varies according to time of session?
A) 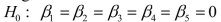
B) 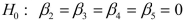
C) 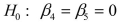
D) 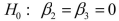
Correct Answer:
Verified
Q111: SCENARIO 18-6 Q111: SCENARIO 18-5 Q131: SCENARIO 18-6 A weight-loss clinic wants to Q131: SCENARIO 18-6 Q132: SCENARIO 18-5 You worked as an intern Q134: SCENARIO 18-5 Q136: SCENARIO 18-5 You worked as an intern Q137: SCENARIO 18-5 Q137: SCENARIO 18-5 You worked as an intern Q138: SCENARIO 18-6 A weight-loss clinic wants to![]()
You worked as an intern at
A weight-loss clinic wants to use
You worked as an intern at
You worked as an intern at
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents