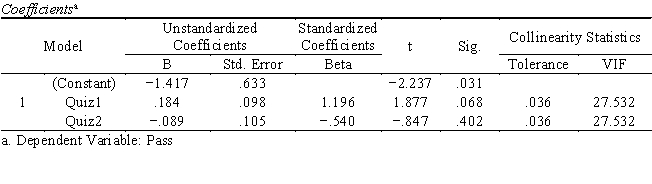
Professor Pruefung Wanted to Examine If Performance in Quizzes Can $\text { Om nibus Tests of Model Coeffcients }$

Professor Pruefung wanted to examine if performance in quizzes can predict whether a student will pass or fail the final exam. The independent variables are scores in two pop quizzes (Quiz1, Quiz2), and the dependent variable is a dichotomous variable (pass = 1 vs. fail = 0). Below is part of the output of the analysis.
a. Professor Pruefung assumed that the better a student performed in the quizzes (a higher score indicates better performance), the higher the odds that he/she will pass the final exam. If that is the case, what are the expected signs for b₁ and b₂? Do the results confirm the expectation?
b. Based on the tables, is there any indication of assumptions violation? If so, which assumption(s) has (have) been violated?
c. What are the possible consequences of the assumption violation?


$\text { Om nibus Tests of Model Coeffcients }$
$\begin{array}{ccccc}\hline & & \text { Chi-square } & d f & \text { Sig. } \\\hline{\text { Step }} & \text { Step } & 24.055 & 2 & .000 \\1 & \text { Block } & 24.055 & 2 & .000 \\& \text { Model } & 24.055 & 2 & .000\end{array}$

$\text { Model Summary }$
$\begin{array}{cccc}\hline {\text { Step }} & {-2 \mathrm{Log}} & \text { Cox \& Snell} & \text {Nagelkerke } \\& \text { likelihood } & R \text { Square } & R \text { Square } \\\hline 1 & 22.998 & .452 & .653\end{array}$
$\begin{array}{l}\text { Variables in the Equation }\\\begin{array}{llllllll}\hline & & \text { B } & \text { S.E. } & \text { Wald } & d f & \text { Sig. } & \operatorname{Exp}(\mathrm{B}) \\\hline {\text { Step 1 }} & \text { Quiz1 } & 1.557 & 1.064 & 2.140 & 1 & .143 & 4.745 \\& \text { Quiz2 } & -.535 & 1.023 & .273 & 1 & .601 & .586 \\& \text { Constant } & -21.721 & 8.990 & 5.838 & 1 & .016 & .000 \\\hline\end{array}\end{array}$