"It is difficult to sustain cooperation in finitely repeated prisoner's dilemma game. Tit-for-tat strategies are key for sustaining cooperation in such situations."
(a) What does finite repetition mean?
(b) Why is it hard to sustain cooperation if the prisoner's dilemma game is repeated finitely?
(c) What does a tit-for-tat strategy imply?
Now we are going to consider an infinitely repeated version of the prisoner's dilemma game shown below.
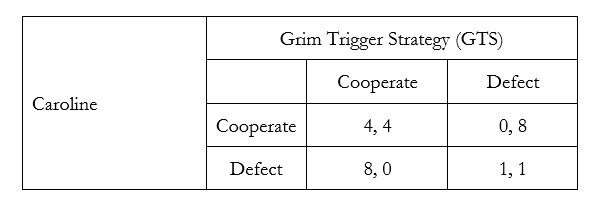
Consider Caroline who is playing against an opponent who relies on a grim-trigger strategy (GTS). This means that if you cooperate GTS will cooperate. But if you ever defect, then GTS will forever defect from the next period on.
Clearly, whether we cooperate or not in such situations is determined by how much we value future payoffs.
If Caroline and GTS keep cooperating, then Caroline keeps getting $4 each period.
If Caroline defects then she gets $8 in that period but because GTS will defect from the next period onward, the best Caroline can hope to get is $1 from the next period onward.
Remember that future payoffs are discounted by (beta*delta), where delta = 1/(1+r) i.e. delta equals {1 over (1+interest rate)}. Here, we will think of "r" as the interest rate that Caroline uses to trade-off between current and future payoffs. For the sake of simplicity assume that there is no inflation and that Caroline's beta is equal to one.
This implies the following sequence of payments for Caroline.
From cooperation: 4 + 4*(delta) + 4*(delta)^2 + 4*(delta)^3 …
From defection: 8 + 1*(delta) + 1*(delta)^2 + 1*(delta)^3…
(d) Consider two values of delta: 0.4 and 0.8. Which one of these is more likely to make Caroline choose "Cooperate" over "Defect" in period 1?
(e) What does the value of delta you identified in Part (1) imply for Caroline's implicit rate of interest? For what value or range of values of the implicit interest rate would Caroline choose to "Cooperate" in period 1?
Correct Answer:
Verified
Q34: In the presence of reciprocal motivations among
Q35: In the context of a public goods
Q36: In the context of a public goods
Q37: Consider a public goods game with 4
Q38: Consider a public goods game with 4
Q40: Andreoni (1988) sets out to distinguish between
Q41: The efficiency implications of costly punishments are
Q42: While punishments may not enhance efficiency in
Q43: Clearly distinguish between what is meant by
Q44: What is the difference between a "partners"
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents