Solved

Let S Be a Piece with Boundary of a Smooth

Question 68

Multiple Choice

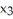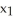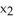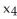Let S be a piece with boundary of a smooth 3-manifold in R4 (hypersurface) given by the equation Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . 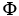Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above = g( Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . 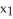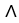Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above , Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above , Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above ) and letLet S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above= d Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above d Let S be a piece with boundary of a smooth 3-manifold in R<sup>4</sup> (hypersurface) given by the equation = g( , , ) and let = d d d . Apart from sign due to orientation of S, is equal to A) the 3-volume of the projection of S onto the hyperplane = 0 B) the 4-volume of the projection of S onto the hyperplane = 0 C) D) E) None of the above 11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d 11ee77e1_7793_6815_a0f8_474d4dbcd8a5_TB9661_11 . Apart from sign due to orientation of S, 11ee77e1_7793_6816_a0f8_97457d751d61_TB9661_11 is equal to


A) the 3-volume of the projection of S onto the hyperplane 11ee77e1_7793_6817_a0f8_13032b247b87_TB9661_11 = 0
B) the 4-volume of the projection of S onto the hyperplane 11ee77e1_7793_6818_a0f8_43b7fef76a07_TB9661_11 = 0
C) 11ee77e1_7793_6819_a0f8_5d277b36f478_TB9661_11
D) 11ee77e1_7793_681a_a0f8_d78a3ae2089d_TB9661_11
E) None of the above

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q63: Find Find ,</p></div><svg width=

Q64: Evaluate the integral of

Q65: If M is the part of the

Q66: Let M be the smooth 2-manifold

Q67: Consider the unit cube Q =

Q69: Use the generalized Stokes's Theorem to find

Q70: Use the generalized Stokes's Theorem to

Q71: Integrate the differential 3-form Integrate</p></div><svg width=

Q72: Let C be the curve of

Q73: State the Divergence Theorem and Stokes's Theorem

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents