Consider the Pair of Functions Y₁ = Ln T and Y₁

Consider the pair of functions y₁ = ln t and y₁ = t ln t.
Which of these statements is true?

A) Both y₁ and y₂ can be solutions of the differential equation on the interval (0, $\infty$ ) , where p(t) and q(t) are continuous on (0, $\infty$ ) .
B) The Wronskian for this function pair is strictly positive on (0, $\infty$ ) .
C) Abel's theorem implies that y₁ and y₂ cannot both be solutions of any differential equation of the form 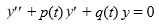on the interval (0, $\infty$ ) .
D) The pair y₁ and y₂ constitutes a fundamental set of solutions to some second-order differential equation of the form 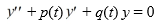on the interval (0, $\infty$ ) .