Which of the Following Is an Accurate Conclusion That Can

Which of the following is an accurate conclusion that can be made using the existence and uniqueness theorem for first-order differential equations for this initial value problem?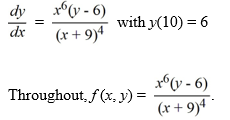

A) The initial value problem has a unique solution because f (x, y) is continuous on a rectangle containing the point (10, 6) .
B) The initial value problem is not guaranteed to have a unique solution because f_x (x, y) is not continuous when x = -9.
C) The initial value problem has a unique solution because both f (x, y) and f_y(x, y) are continuous on a rectangle containing the point (10, 6) .
D) The initial value problem does not have a solution because f_x (x, y) and f_y (x, y) are not both continuous on a rectangle containing the point (10, 6) .