Consider Two Vector Fields $\vec{U}$ And $\vec{W}$ at Every Point in Space

Consider two vector fields $\vec{U}$ and $\vec{W}$ . At every point in space, $\vec{U}$ points vertically upward, while $\vec{W}$ points radially away from some central point. But $|\vec{U}|=|\vec{W}|=$ a fixed constant everywhere. Assume that we calculate the flux of $\vec{U}$ and $\vec{W}$ through hemispherical surfaces having the same size and orientation, as shown below. Assume that the tile vectors on each surface point outward. Also assume that in the right-hand case, the central point from which the field $\vec{W}$ radiates is at the center of the flat plane at the bottom of the hemisphere. Do not assume that these fields necessarily represent particle flows.

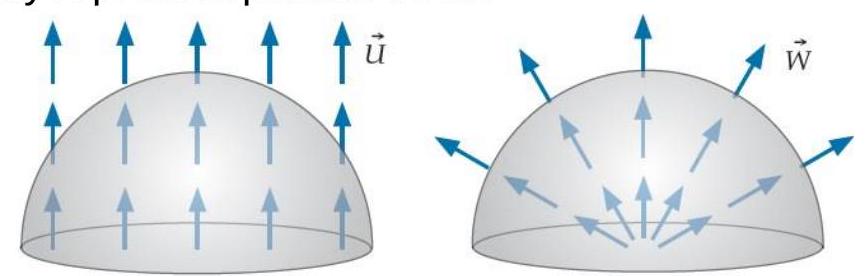
How do the fluxes of these fields through the two identical hemispherical surfaces compare?
A. Field $\vec{U}$ has the larger flux.
B. Field $\vec{W}$ has the larger flux.
C. Both fields have the same flux.
D. The result depends on the surface's radius.
E. We need more information to compare the fluxes.