Consider the game depicted below.Player 1 decides between going L or R in stage 1 and 3 of the game.Player 2 decides between going l and r in stage 2 of the game. 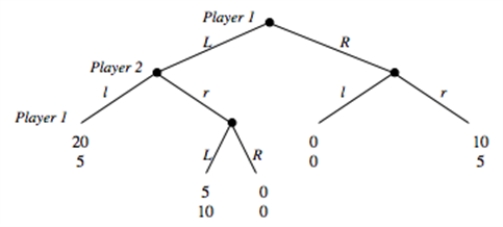
a.List the possible pure strategies for each player in this game and illustrate the payoffs from each pair of strategies in a matrix.
b.Is there a dominant strategy for either player?
c.Identify the subgame perfect equilibrium strategies and outcome.
d.Identify the Nash Equilibria that are not subgame perfect.
e.For each Nash Equilibrium that is not subgame perfect, explain which parts of the Nash Equilibrium strategies are non-credible.f.Suppose you have developed a drug that can be administered without the victim being aware of it.The effect of the drug is that the victim suddenly becomes gullible and believes anything he is told.You only have 1 dose of the drug and decide to auction it off to the two players right before they play each other in the game you have analyzed so far.Each player is asked to submit a sealed bid, and the highest bidder will be sold the drug at a price equal to the highest bid.In case of a tie in bids, a coin is flipped to determine who wins and pays the price that was bid.Suppose in this part that payoffs are in terms of dollars and that bids can be made in one cent increments.Suppose further that players do not consider bidding above the maximum they are willing to pay.Given that the players know each other's payoffs in the above game, what is the equilibrium price that you will be able to sell the drug for? (Hint: There are two possible answers.)
g.In part (f), we said "Suppose further that players do not consider bidding above the maximum they are willing to pay." Can you think of a Nash equilibrium to the auction that would end in a price of $8 if we had not made that statement in (f)?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q27: A dominant strategy is one that is
Q28: Dominant strategy Nash equilibria are efficient.
Q29: If a player's strategy in a sequential
Q30: A Prisoner's Dilemma game is one in
Q31: If a pooling equilibrium is played in
Q32: Suppose player 1 potentially moves twice in
Q34: If we depict a simultaneous move, complete
Q35: Consider the following sequential move game:
Q36: If there is no pure strategy Nash
Q37: Consider player n in a sequential game.
a.If
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents