Solved

At Prices (P1, P2) = ($4, $2), Ivan Buys the Bundle

Question 51

Multiple Choice

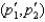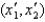At prices (p1, p2) = ($4, $2) , Ivan buys the bundle (x1, x2) = (8, 20) . At prices At prices (p<sub>1</sub>, p<sub>2</sub>) = ($4, $2) , Ivan buys the bundle (x<sub>1</sub>, x<sub>2</sub>) = (8, 20) . At prices = ($2, $4) , he buys the bundle = (10, 13) . At prices , he buys the bundle = (14, 11) . If his preferences satisfy the strong axiom of revealed preferences, then it must be that A) 8p<sub>1</sub> > 2p<sub>2</sub>. B) 6< 9. C) 6< 8. D) =. E) None of the above. 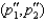= ($2, $4) , he buys the bundle At prices (p<sub>1</sub>, p<sub>2</sub>) = ($4, $2) , Ivan buys the bundle (x<sub>1</sub>, x<sub>2</sub>) = (8, 20) . At prices = ($2, $4) , he buys the bundle = (10, 13) . At prices , he buys the bundle = (14, 11) . If his preferences satisfy the strong axiom of revealed preferences, then it must be that A) 8p<sub>1</sub> > 2p<sub>2</sub>. B) 6< 9. C) 6< 8. D) =. E) None of the above. = (10, 13) . At prices At prices (p<sub>1</sub>, p<sub>2</sub>) = ($4, $2) , Ivan buys the bundle (x<sub>1</sub>, x<sub>2</sub>) = (8, 20) . At prices = ($2, $4) , he buys the bundle = (10, 13) . At prices , he buys the bundle = (14, 11) . If his preferences satisfy the strong axiom of revealed preferences, then it must be that A) 8p<sub>1</sub> > 2p<sub>2</sub>. B) 6< 9. C) 6< 8. D) =. E) None of the above. , he buys the bundle At prices (p<sub>1</sub>, p<sub>2</sub>) = ($4, $2) , Ivan buys the bundle (x<sub>1</sub>, x<sub>2</sub>) = (8, 20) . At prices = ($2, $4) , he buys the bundle = (10, 13) . At prices , he buys the bundle = (14, 11) . If his preferences satisfy the strong axiom of revealed preferences, then it must be that A) 8p<sub>1</sub> > 2p<sub>2</sub>. B) 6< 9. C) 6< 8. D) =. E) None of the above. = (14, 11) . If his preferences satisfy the strong axiom of revealed preferences, then it must be that


A) 8p1 > 2p2.
B) 6< 9.
C) 6< 8.
D) =.
E) None of the above.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q43: Hillary has an initial endowment of $500

Q44: Hillary has an initial endowment of $500

Q46: Consider the case of Ronald. Let the

Q50: Consider the case of Ronald. Let the

Q50: Franco and Gianni have the same tastes

Q51: Pierre's friend Henri lives in a town

Q53: If Goldie chooses the bundle (6, 6)

Q54: On the planet Homogenia, every consumer who

Q55: On the planet Hyperion, every consumer who

Q56: On the planet Hyperion, every consumer who

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents