A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is 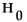
: 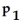
= 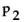
and the alternative is 
: 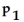
≠ 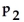
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-A poll reported that 30% of 60 Canadians between the ages of 25 and 29 had started saving money for retirement.Of the 40 Canadians surveyed between the ages of 21 and 24,25% had started saving for retirement.
A) P-value = 0.5824;There is about a 58.24% chance that the two proportions are equal.
B) P-value = 0.1812;If there is no difference in the proportions,there is about a 18.12% chance of seeing the observed difference or larger by natural sampling variation.
C) P-value = 0.2912;There is about a 24.96% chance that the two proportions are equal.
D) P-value = 0.2912;If there is no difference in the proportions,there is about a 24.96% chance of seeing the exact observed difference by natural sampling variation.
E) P-value = 0.5824;If there is no difference in the proportions,there is about a 58.24% chance of seeing the observed difference or larger by natural sampling variation.
Correct Answer:
Verified
Q19: A study was conducted to determine if
Q20: A researcher wishes to determine whether the
Q21: A poll reported that 3 out of
Q21: Use the traditional method to test the
Q23: A study investigated the smoking status of
Q24: A marketing survey involves product recognition in
Q26: Use the given sample data to test
Q28: A new manager,hired at a large warehouse,was
Q30: In a random sample of 360 women,65%
Q34: A weight loss centre in the city
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents