You Have Collected Data from Major League Baseball (MLB)to Find $\widehat{\text { Winpct} }$

You have collected data from Major League Baseball (MLB)to find the determinants of winning. You have a general idea that both good pitching and strong hitting are needed to do well. However, you do not know how much each of these contributes separately. To investigate this problem, you collect data for all MLB during 1999 season. Your strategy is to first regress the winning percentage on pitching quality ("Team ERA"), second to regress the same variable on some measure of hitting ("OPS - On-base Plus Slugging percentage"), and third to regress the winning percentage on both.
Summary of the Distribution of Winning Percentage, On Base plus Slugging Percentage,
and Team Earned Run Average for MLB in 1999 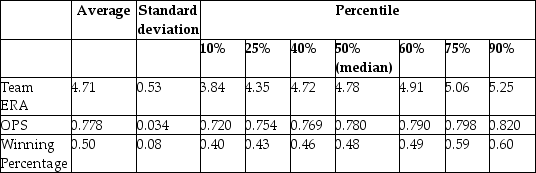The results are as follows: $\widehat{\text { Winpct} }$ = 0.94 - 0.100 × teamera, R² = 0.49, SER = 0.06.
(0.08)(0.017) $\widehat{\text { Winpct }}$ = -0.68 + 1.513 × ops, R²=0.45, SER = 0.06.
(0.17)(0.221) $\widehat{\text { Winpct }}$ = -0.19 - 0.099 × teamera + 1.490 × ops, R²=0.92, SER = 0.02.
(0.08)(0.008)(0.126)
(a)Use the t-statistic to test for the statistical significance of the coefficient.
(b)There are 30 teams in MLB. Does the small sample size worry you here when testing for significance?